Metoda 4M – 4M-BASE-v2n

Metoda 4M – 4M-BASE-v2n « « (Update: 20-12-2024 22:39)

4M-BASE-v2n – wersja rozbudowana

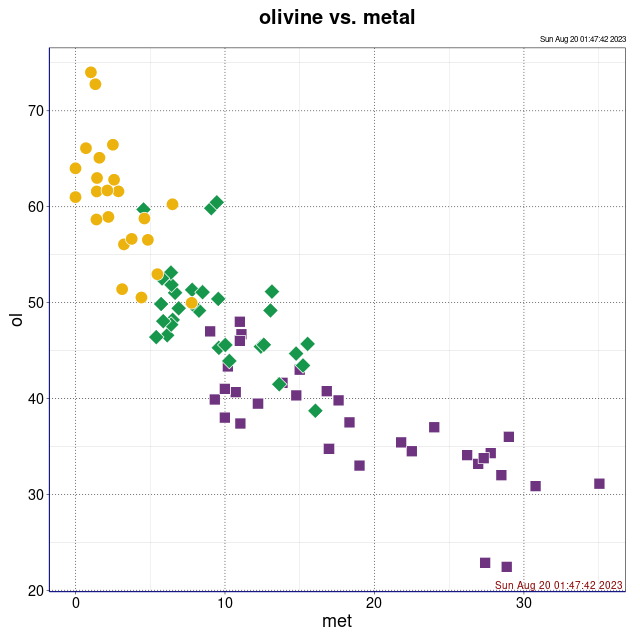
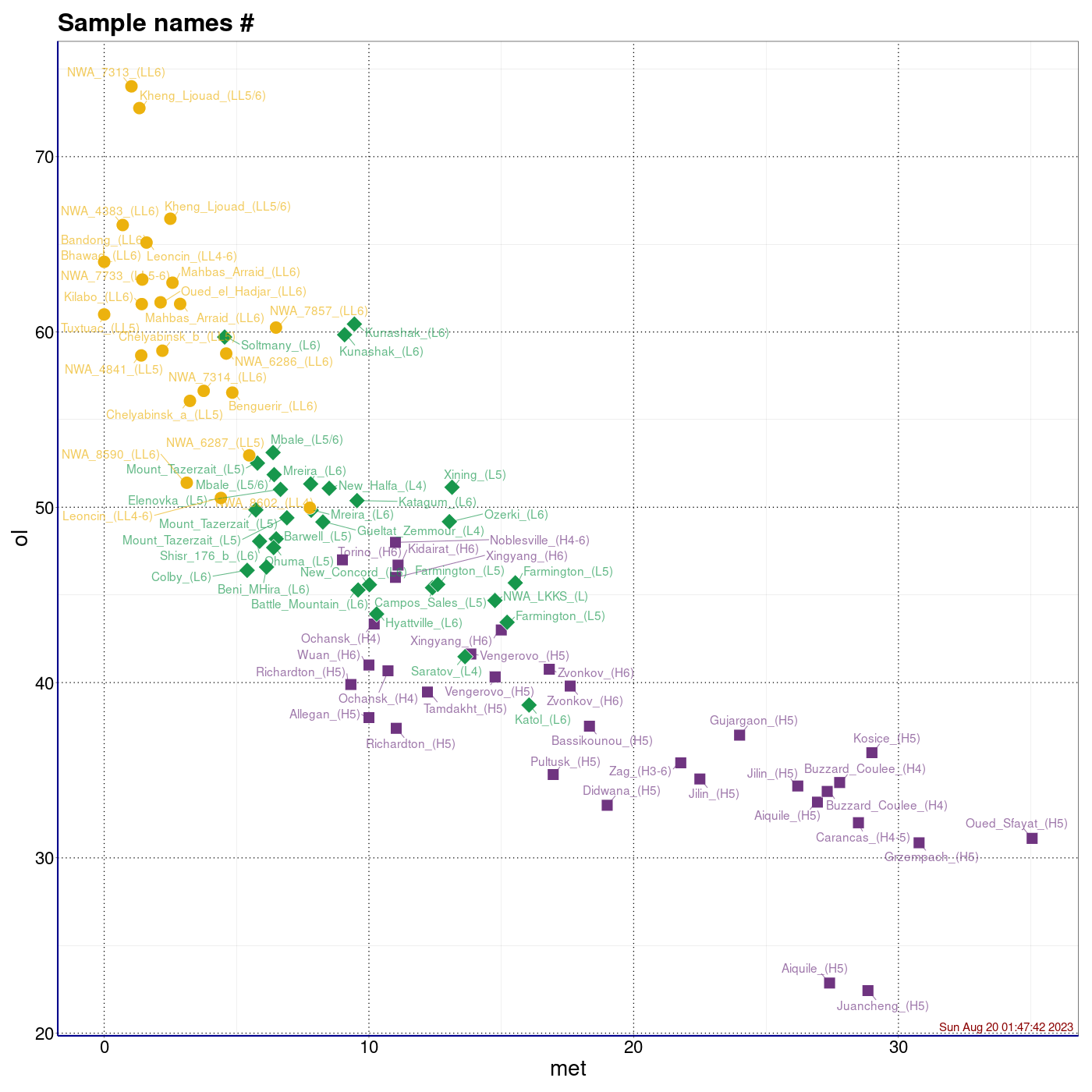
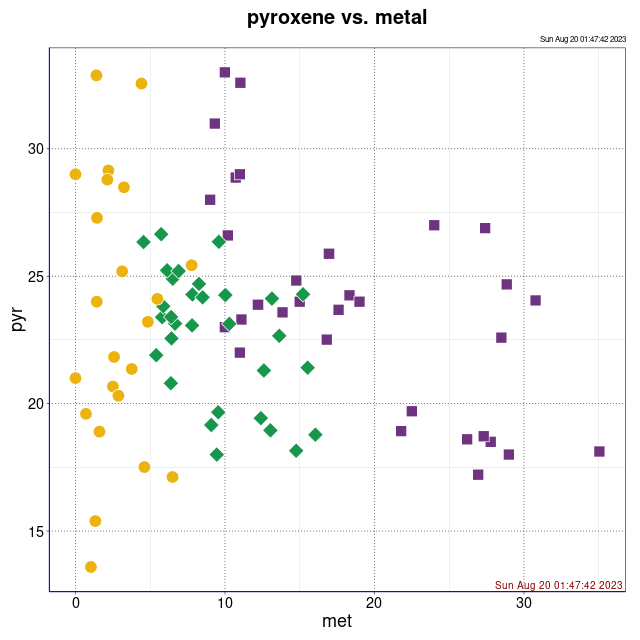
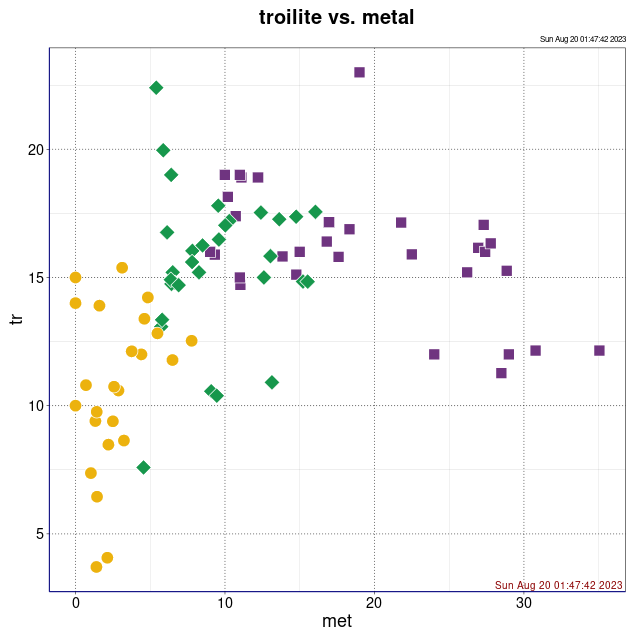
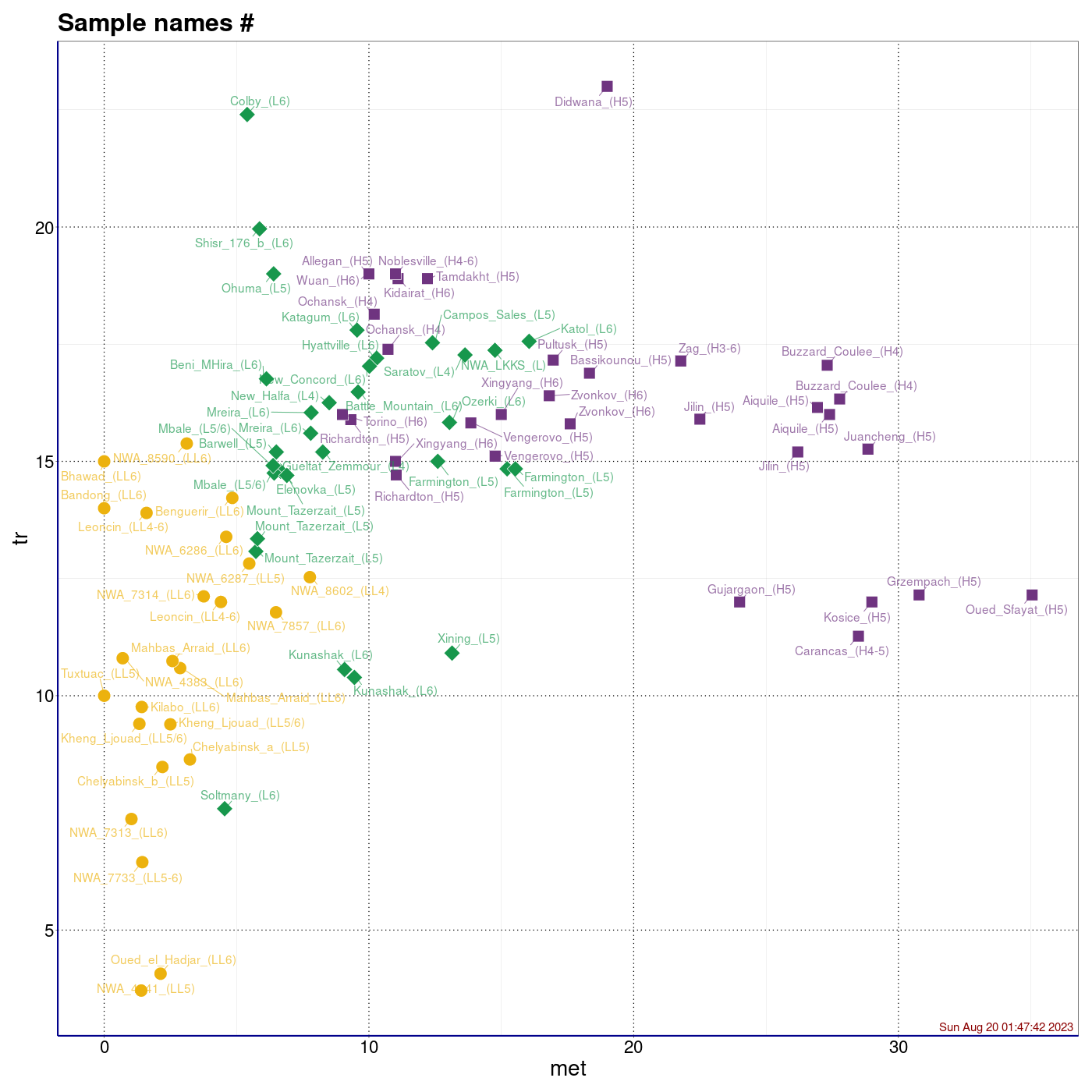
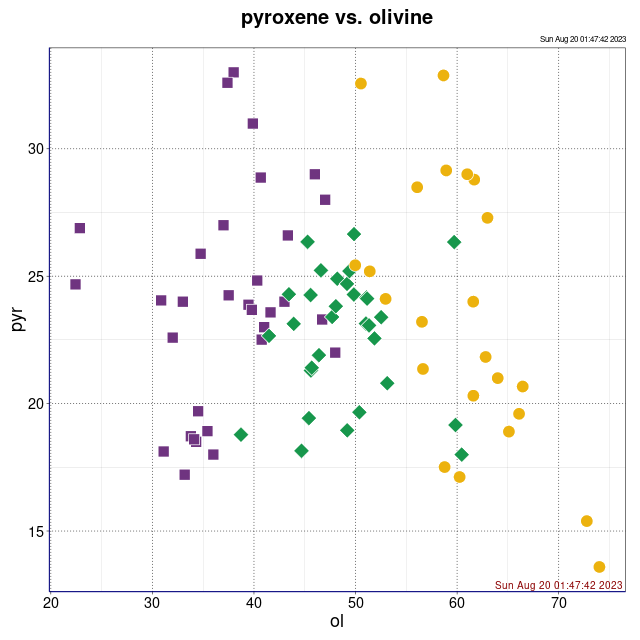
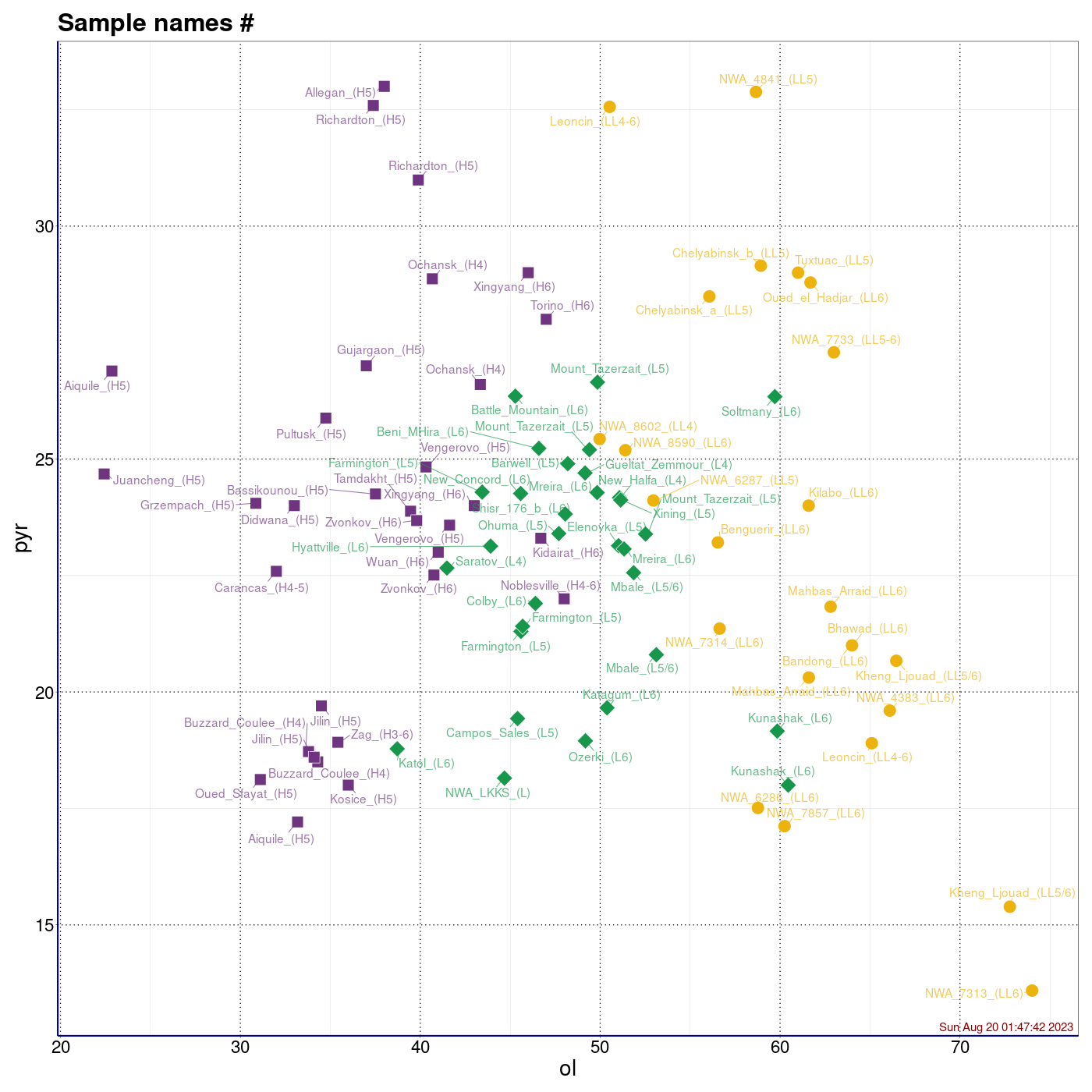
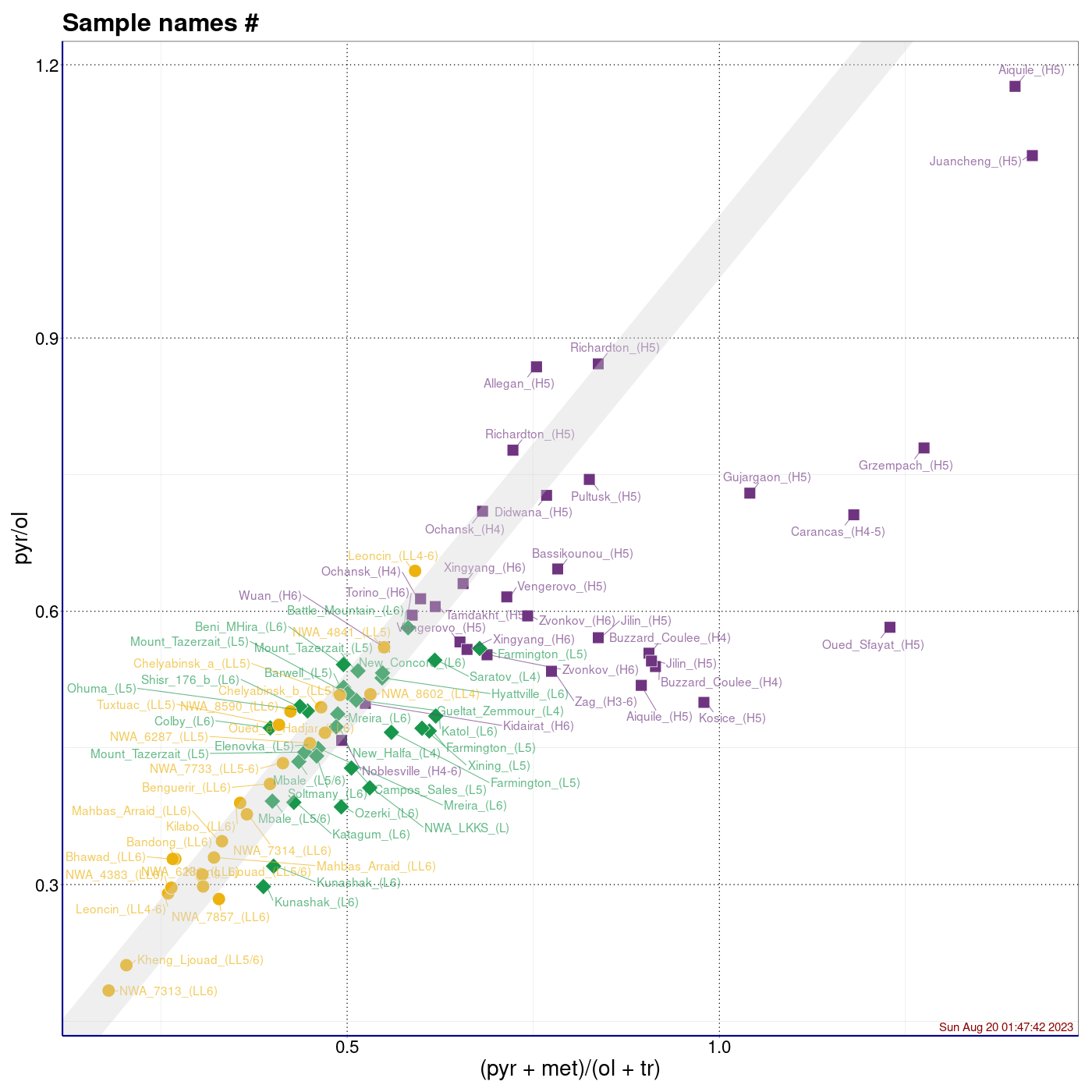
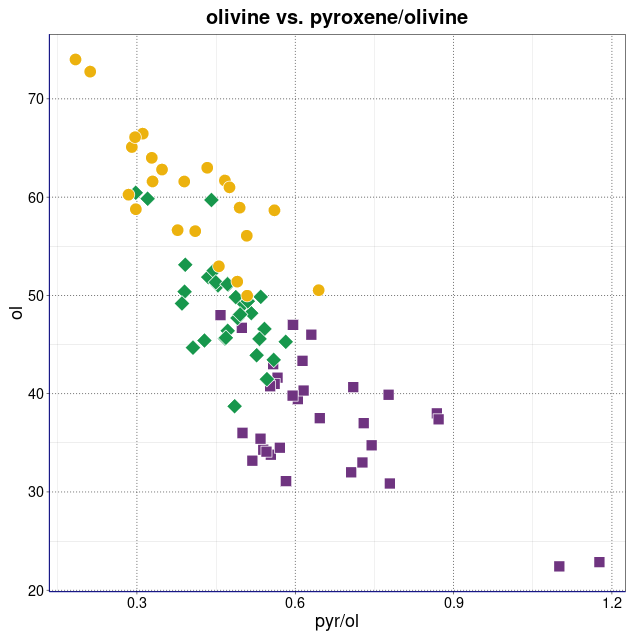
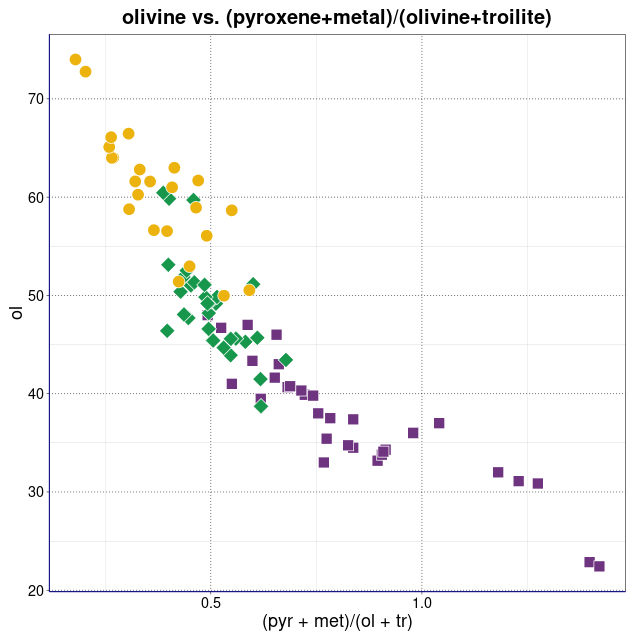
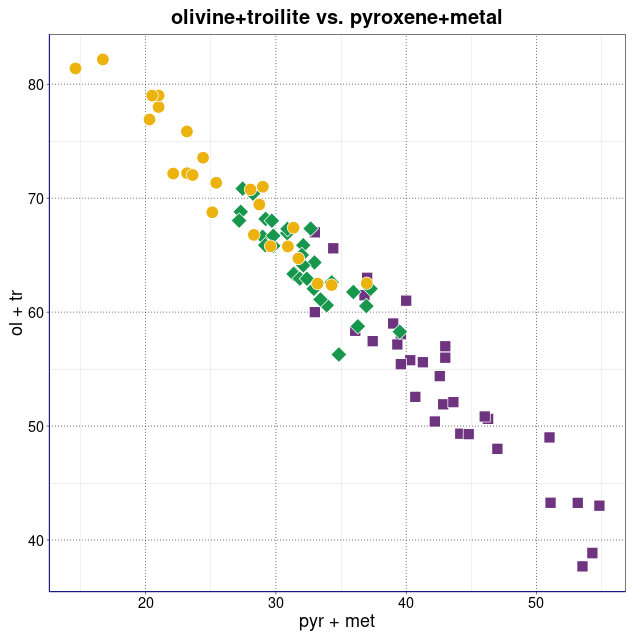
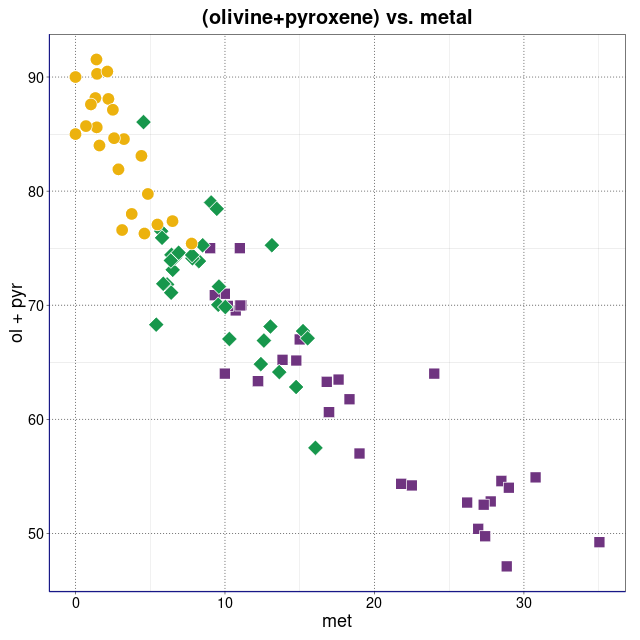
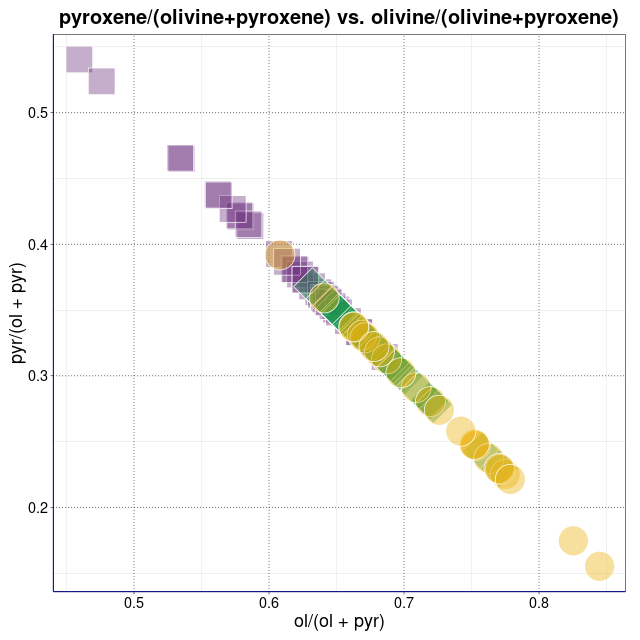
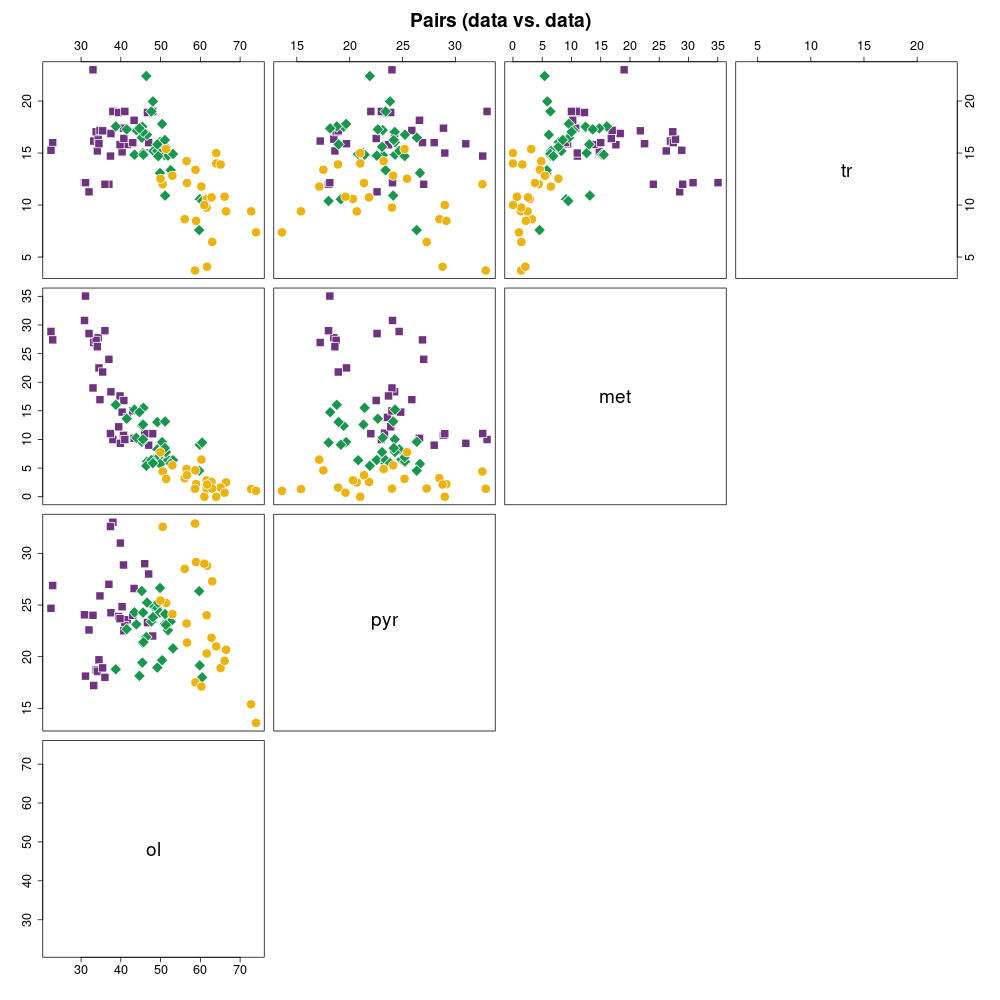
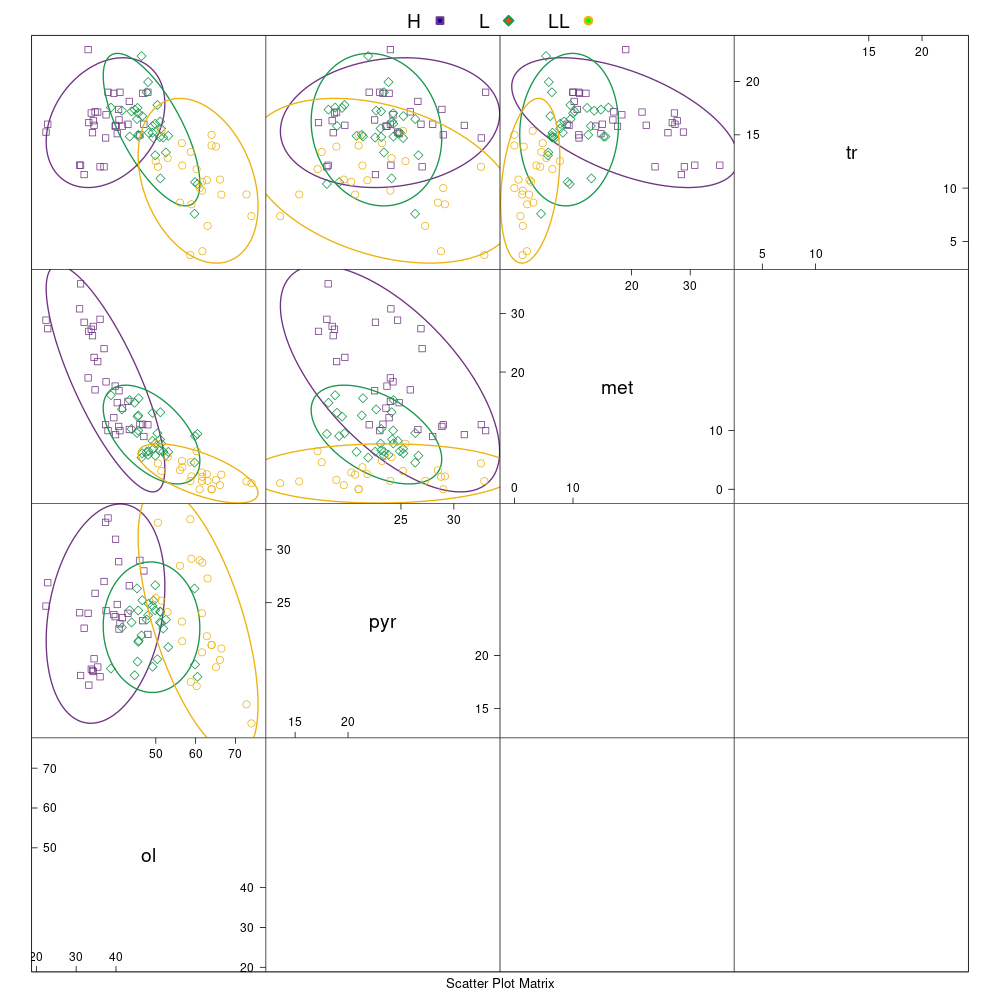
Procentowości podwidm mössbauerowskich chondrytów zwyczajnych.

Wykresy (statystyki):

pairs;
ellipses;
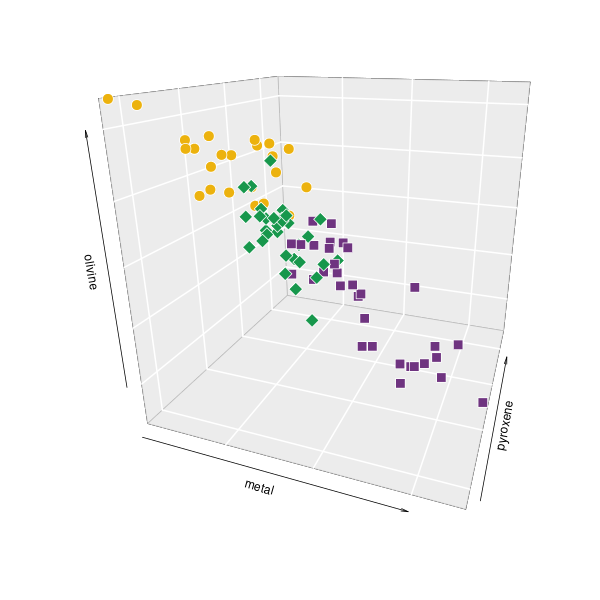
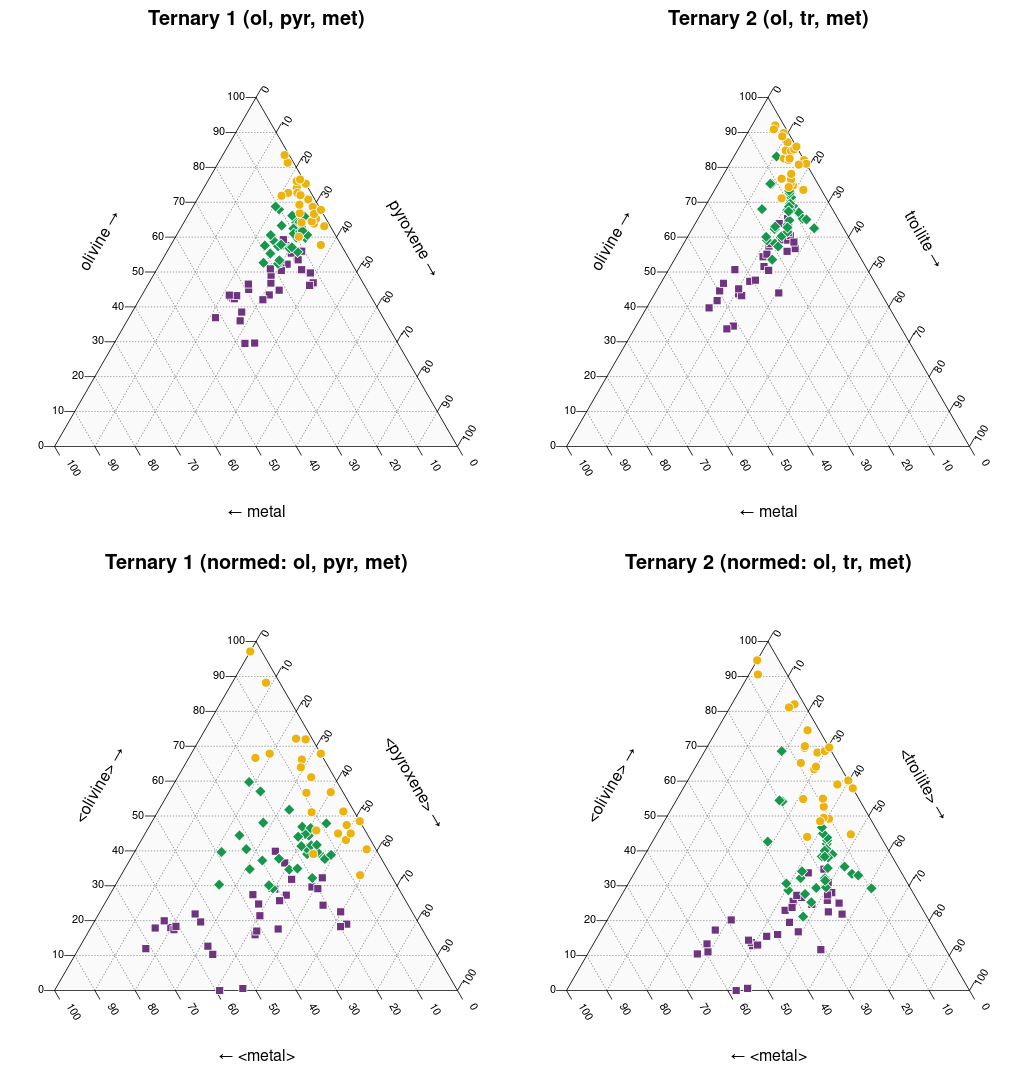
trójkątny (ternary plot);
Voronoi diagrams;
gęstości prawdopodobieństwa (probability density function) i pudełkowy z wąsami (box and whisker);
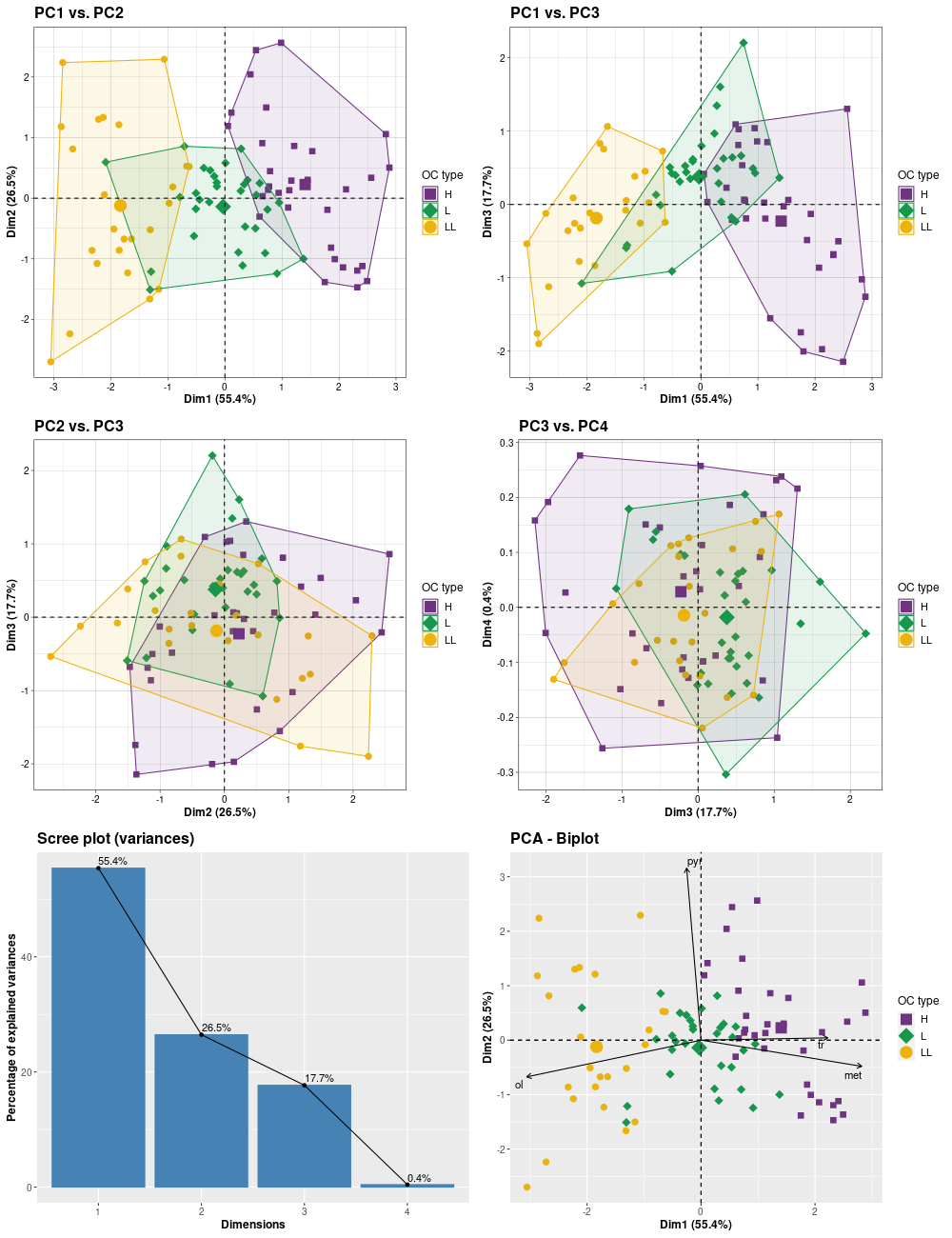
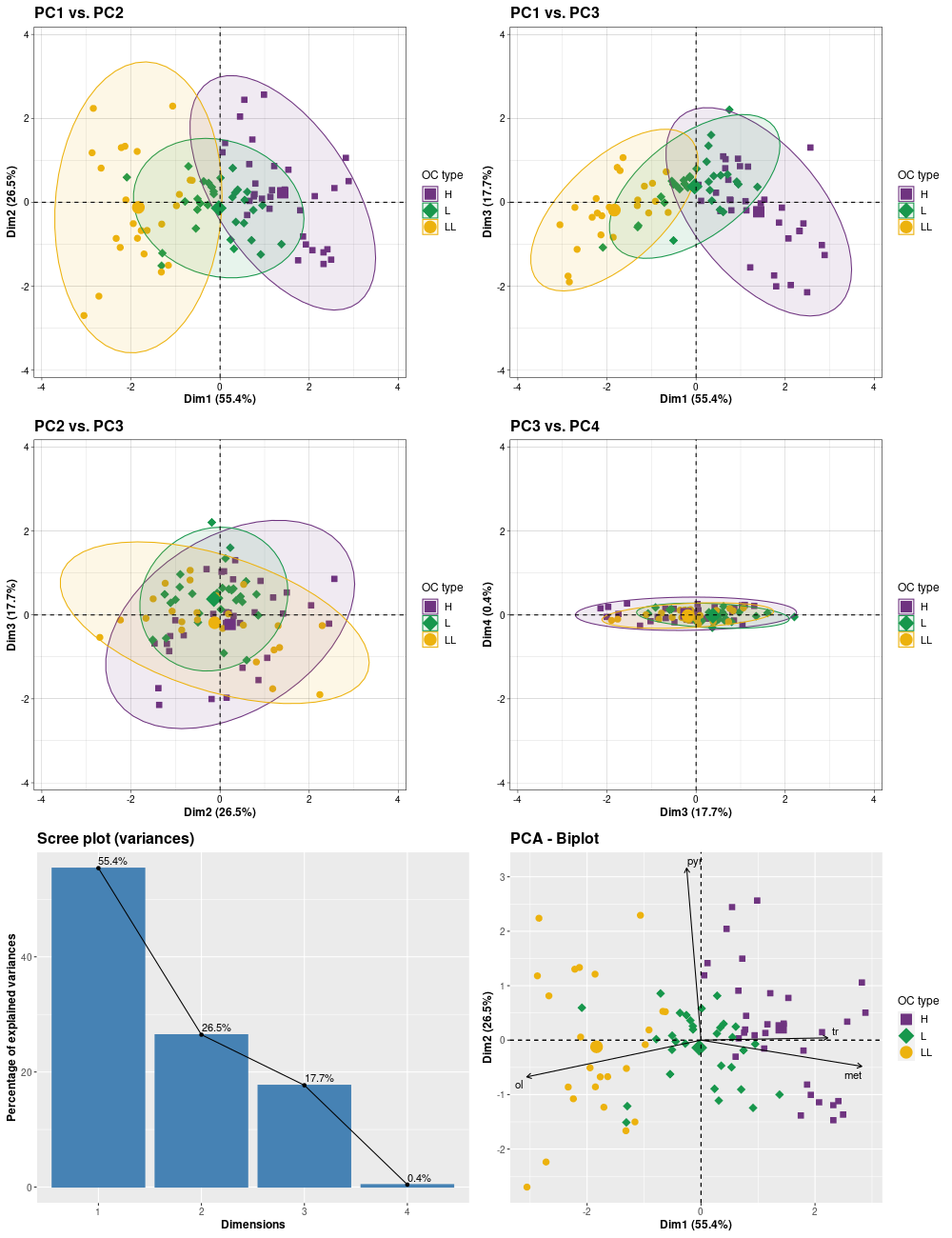
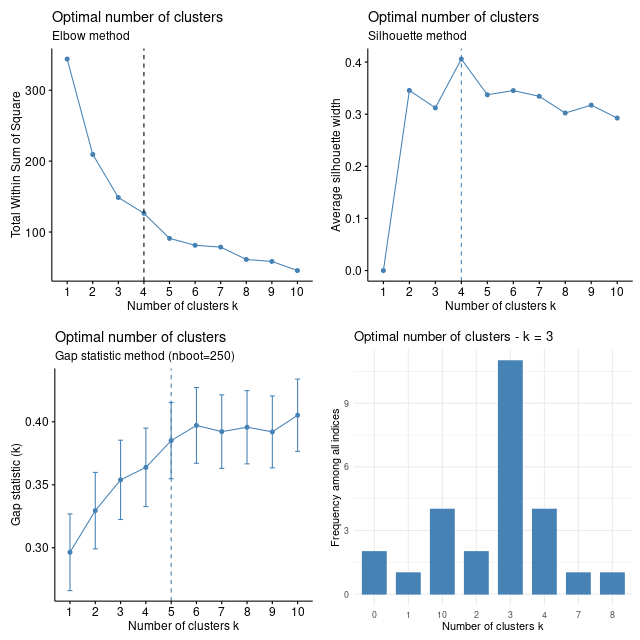
składowych głównych (Principal Component Analysis, PCA);
BASE points classification - k-medoids clustering;
BASE points classification - 4M method clustering (pie);
BASE points classification - Bayes classification rule (pie);
symulacje;
analiza aglomeracyjna (cluster analysis).

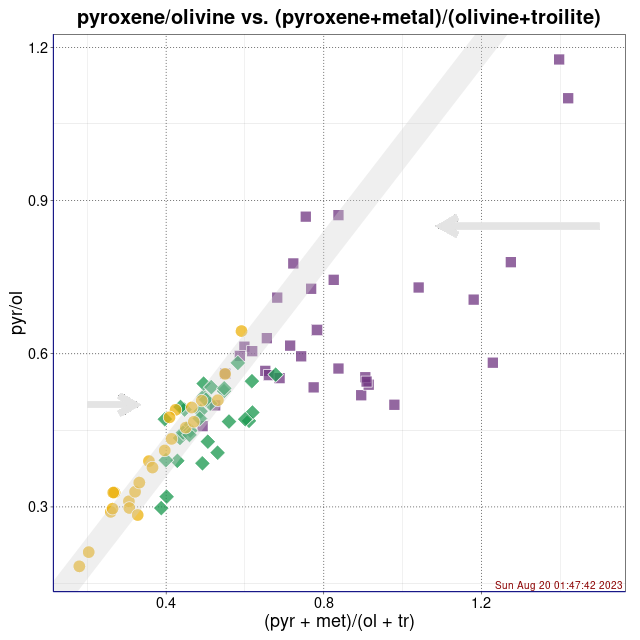
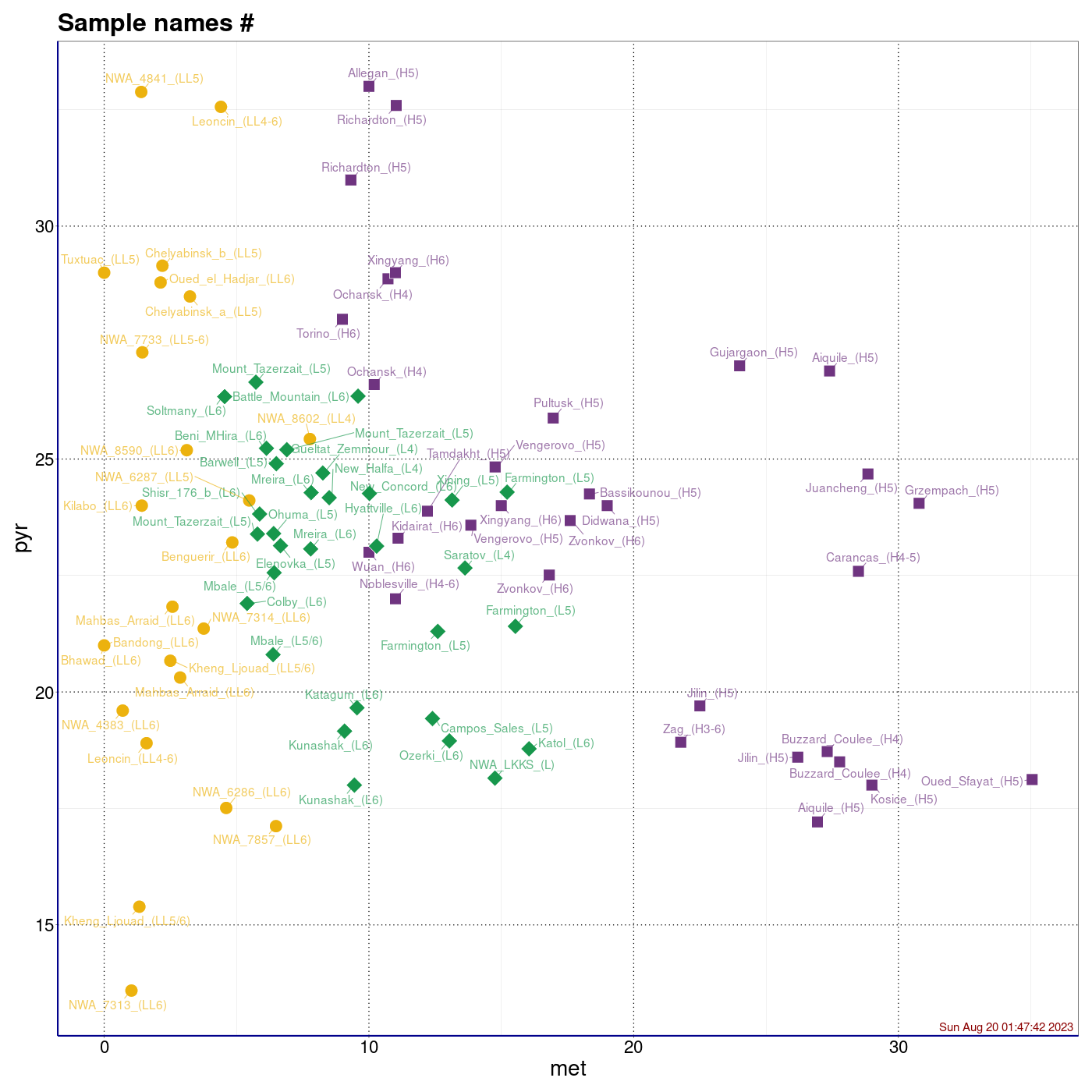
Legenda: Chondryty zwyczajne typu H (■), L (♦), LL (●) oraz wartości średnie i centroidy klastrów (+)

olivine vs. metal (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

metal vs. olivine (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

oliwin vs. metal (wykres sporządzony w pakiecie statystycznym R)

pyroxene vs. metal (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

metal vs. pyroxene (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

piroksen vs. metal (wykres sporządzony w pakiecie statystycznym R)

troilite vs. metal (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

metal vs. troilite (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

troilit vs. metal (wykres sporządzony w pakiecie statystycznym R)

pyroxene vs. olivine (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

piroksen vs. oliwin (wykres sporządzony w pakiecie statystycznym R)

pyroxene/olivine vs. (pyroxene+metal)/(olivine+troilit) (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

piroksen/oliwin vs. (piroksen+metal)/(oliwin+troilit) (wykres sporządzony w pakiecie statystycznym R)

Varia. Kombinacje piroksen+metal/oliwin+troilit i inne (wykresy sporządzone w pakiecie statystycznym R)

Pairs (BASE-v2n)

pairs (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

Wykres wszyscy-ze-wszystkimi (pairs)
(wykres sporządzony w pakiecie statystycznym R)

Ellipses (BASE-v2n)

ellipse (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

Wykres ellipse (wykres sporządzony w pakiecie statystycznym R)
(wielkość elips odpowiada poziomowi istotności 95% - 1,96σ)

Voronoi diagrams (BASE-v2n)

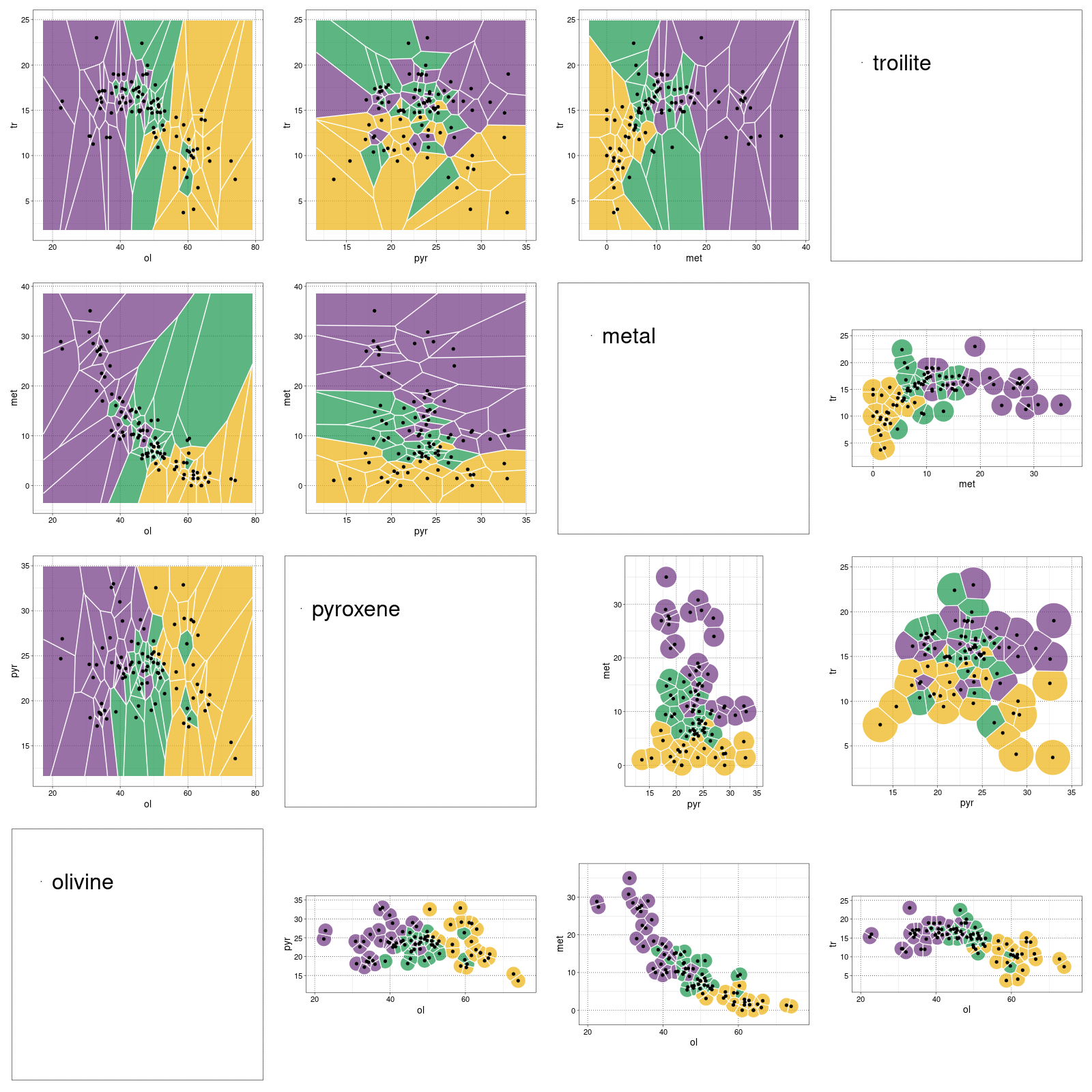
Voronoi diagram. Wykres zainspirowany opisywanymi w literaturze pomysłami prostego podziału przestrzeni cech na rozłączne obszary zawierające meteoryty tylko jednego typu. Pierwotnie pomysł zaproponował Verma et al., a nadal rozwija go Oshtrakh et al. (sources)
(wykres sporządzony w pakiecie statystycznym R)

set BASE - Voronoi diagram animation (worm ;-)

Specjalnie dla naszych miłych Pań - "robak Woronoja"

Ternary (BASE-v2n)

Ternary plot (Multidimensional discriminant analysis and Mahalanobis distance — 4M method (meteorites-Mössbauer-multidimensional-Mahalanobis))

Wykres trójkątny (ternary plot) na którym doskonale widać potencjał dyskryminacyjny parametrów mössbauerowskich
(wykres sporządzony w pakiecie statystycznym R)

Density, box and whisker (BASE-v2n)

density (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

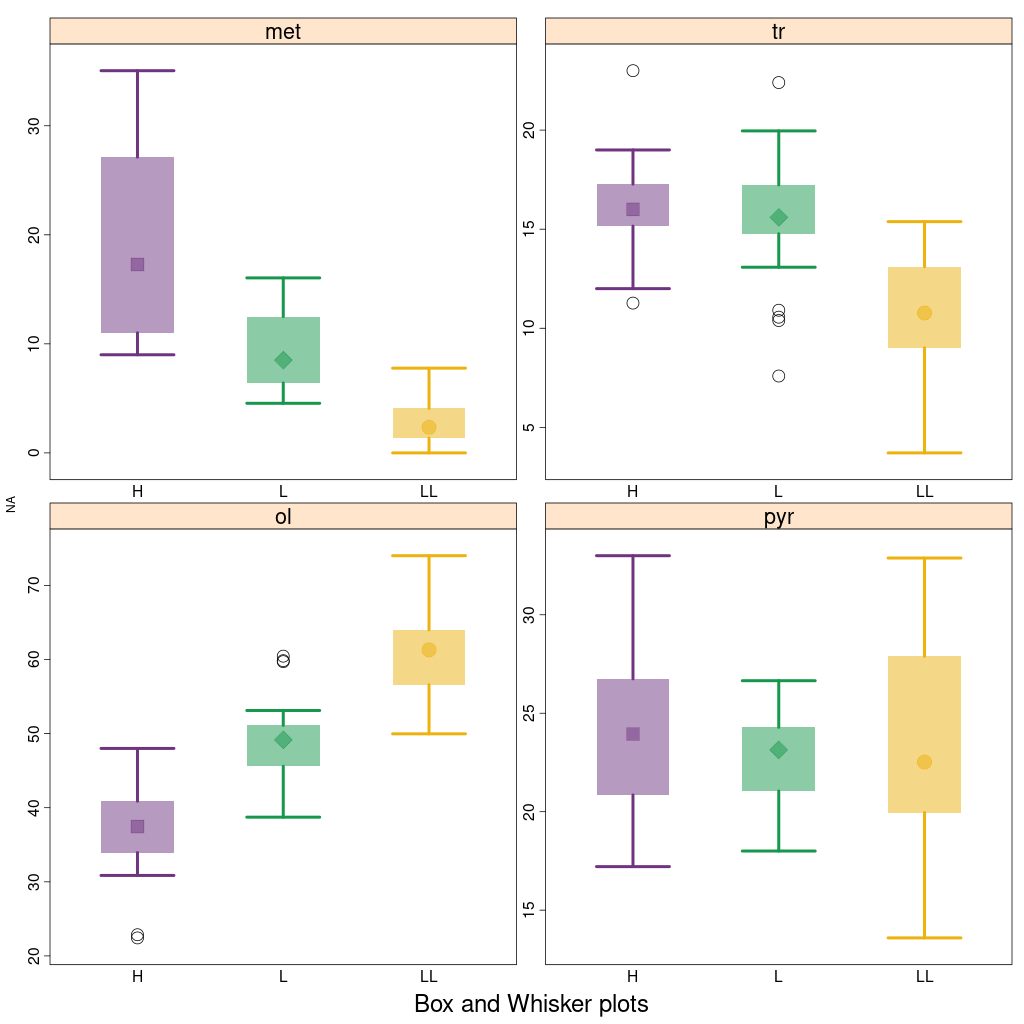
box (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

Wykresy density - wykresy oszacowania gęstości rozkład danych. Podobnie jak histogram, podsumowuje się zależność między wartościami parametrów a liczbą obserwacji, ale zamiast częstotliwości podsumowuje się ją jako ciągłą funkcję gęstości prawdopodobieństwa (probability density function, PDF). Jest to prawdopodobieństwo, że dana obserwacja ma określoną wartość.
Wykresy box and whisker - wykresy pudełkowe i wąsy podsumowują rozkład danego parametru; pokazują ramkę dla 1 i 3 kwartyla, linię w ramce (?!) dla 50. centyla (medianę) i kropkę dla średniej. Wąsy pokazują 1,5 × wysokość prostokąta (zwanego przedziałem między kwartylami, interquartile range, IQR), co wskazuje oczekiwany zakres danych, a wszelkie dane poza tymi wąsami są uznawane za wartości odstające i oznaczone kropką.
(wykres sporządzony w pakiecie statystycznym R)

PCA - Principal Component Analysis (BASE-v2n)

Principal Component Analysis (PCA)

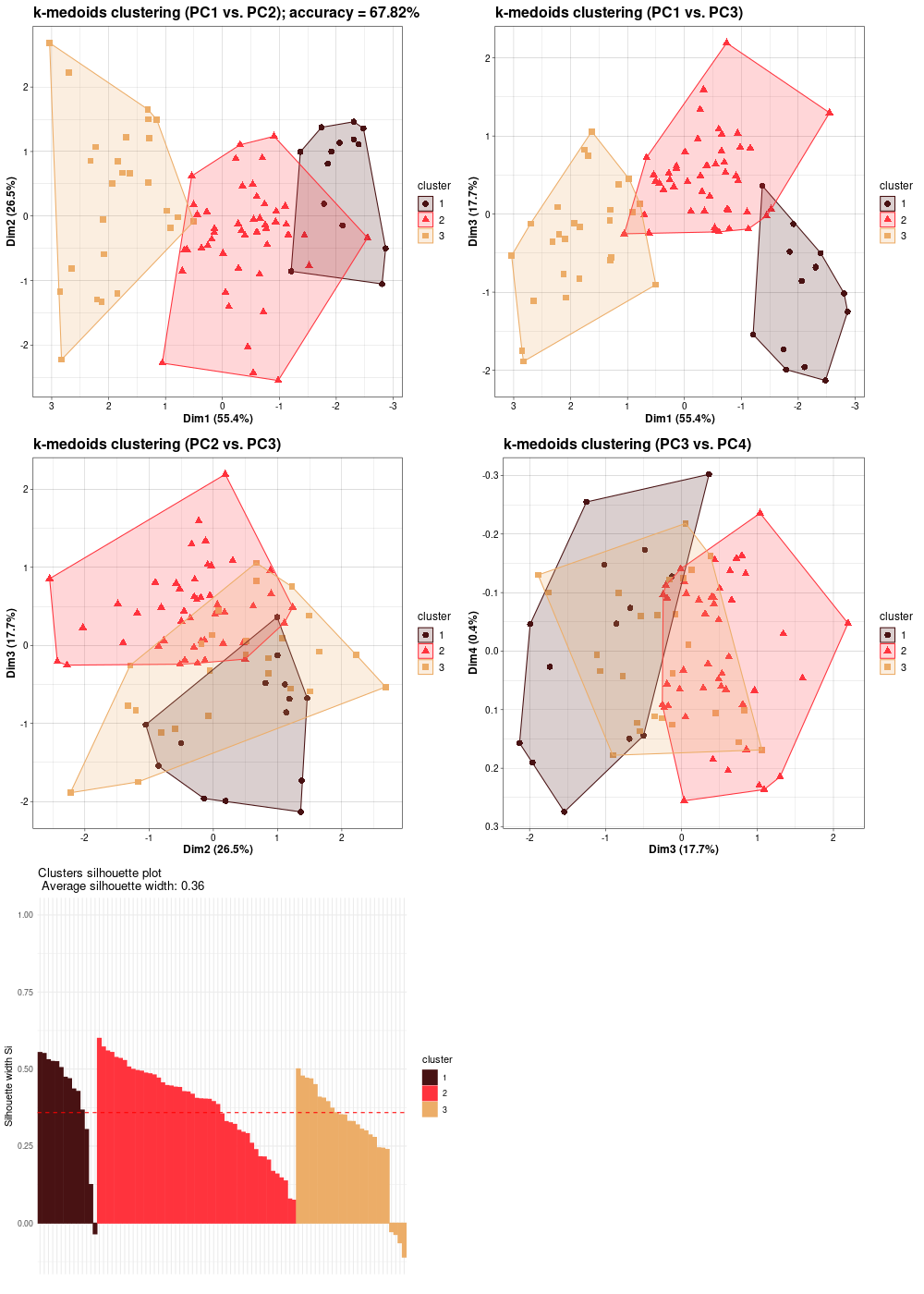
BASE points classification - k-medoids clustering (BASE-v2n)

Optimal number of clusters

See → Cluster analysis - dendogram

k-medoids clustering

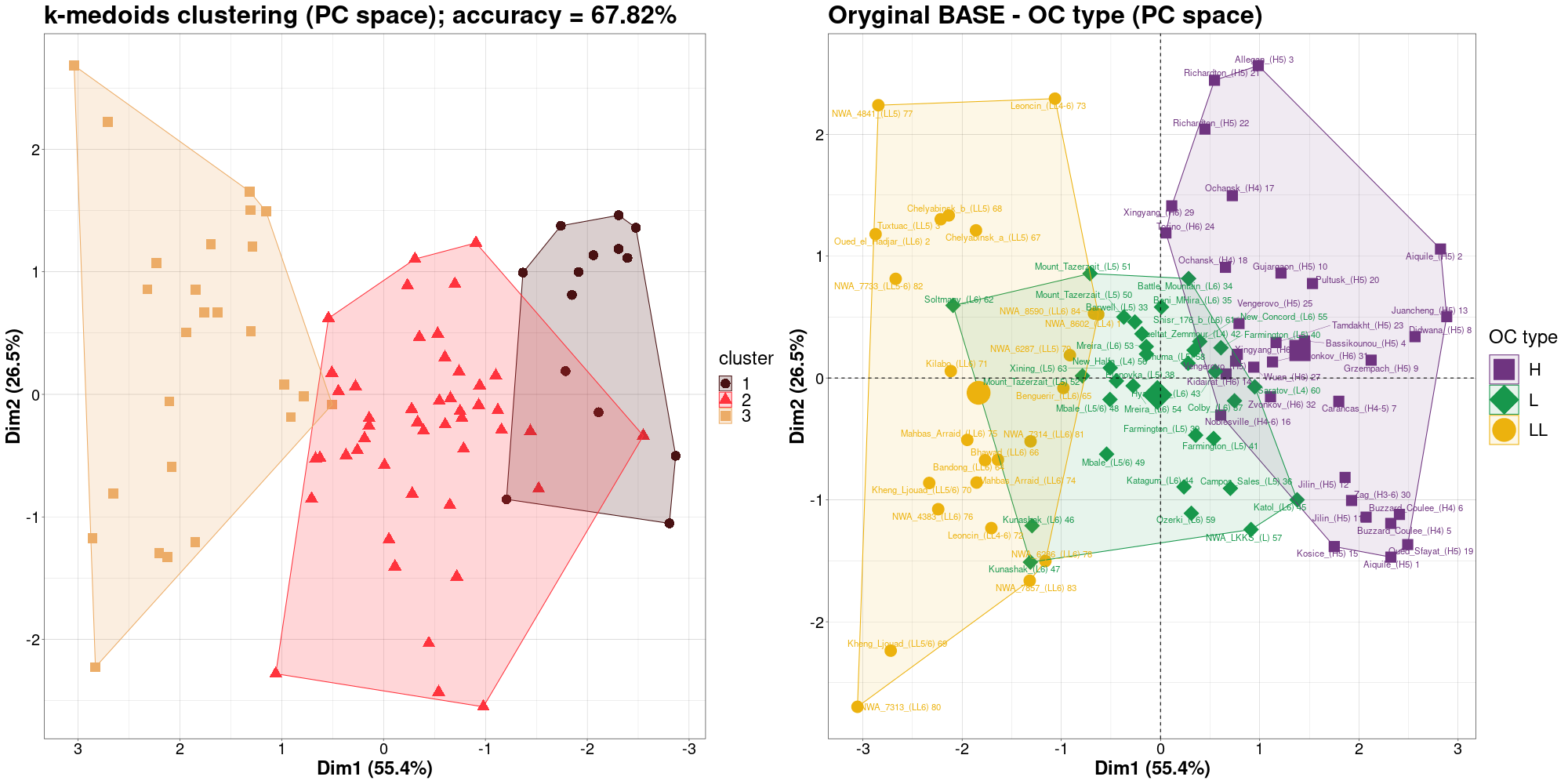
k-medoids clustering in PCA view (version HiRes)

BASE points classification - 4M method clustering (BASE-v2n)

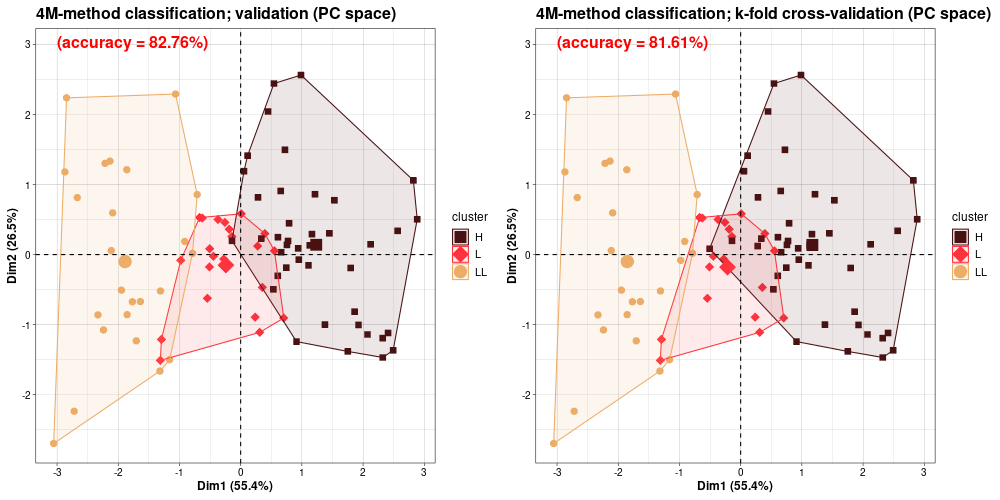
4M-method clustering in PCA view

...compare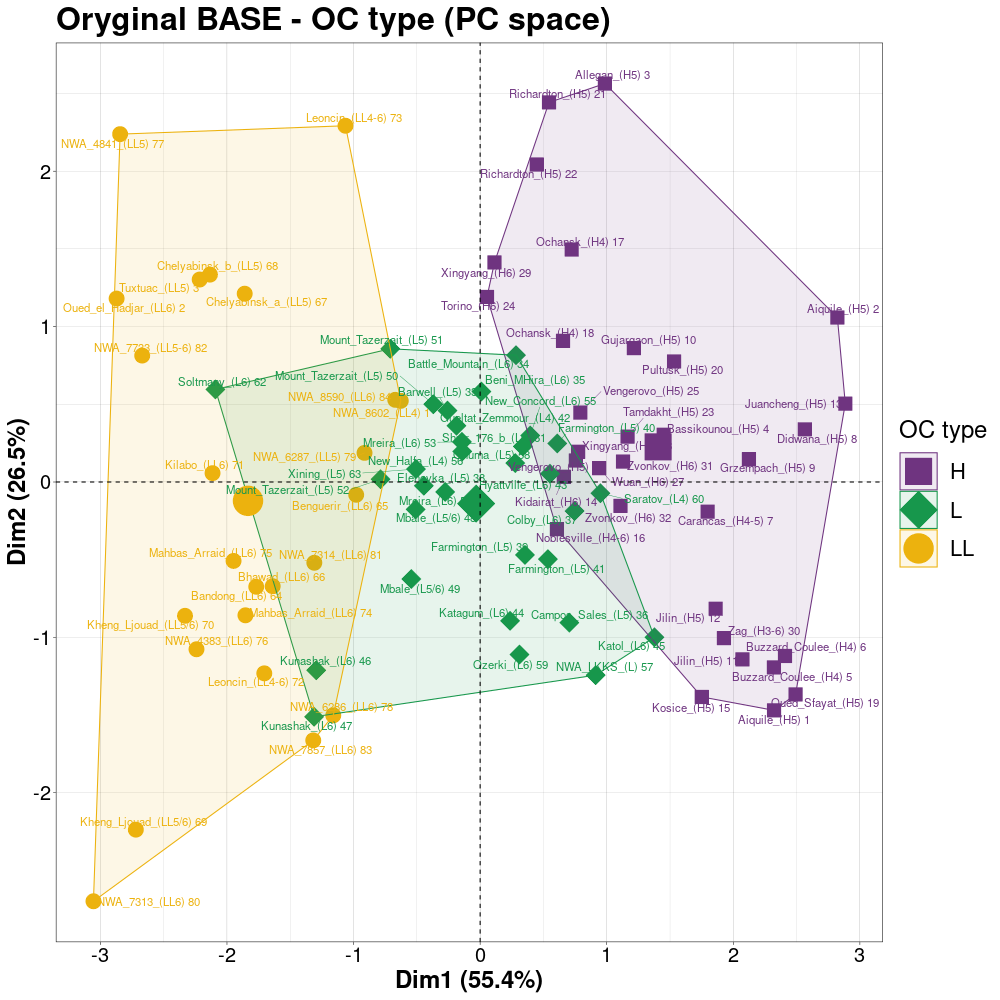

(version HiRes)



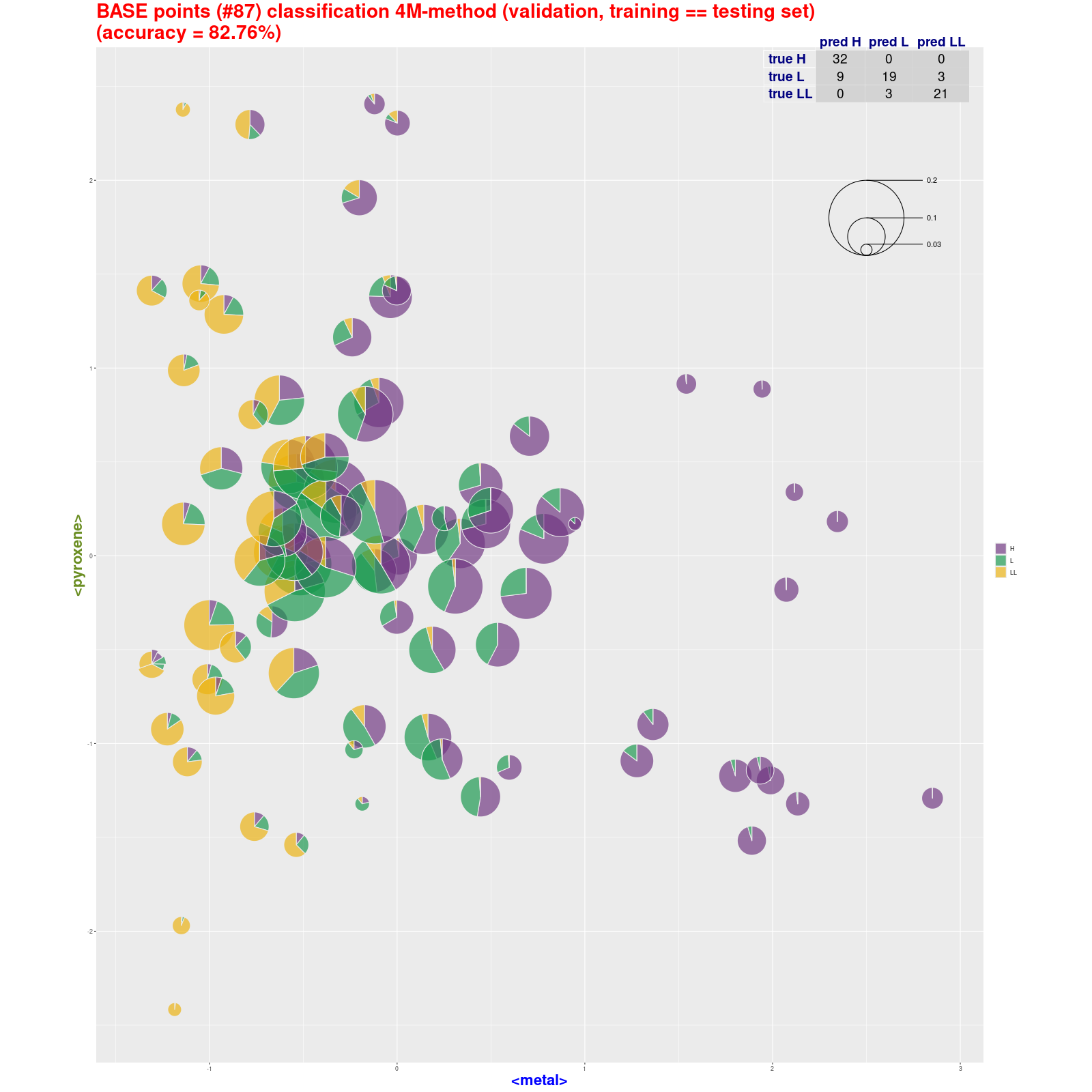
*BASE points classification - 4M-method (pie)* (validation, training ≡ testing set) weryfikacja, zbiór testowy ≡ zbiór uczący Rewelacyjna trafność (accuracy) klasyfikacji! (klasyfikacja nienadzorowana metodą k-medoids miała dużo gorszy współczynnik trafności accuracy <70%) Patrz również → symulacje Tabela z wynikami klasyfikacji.
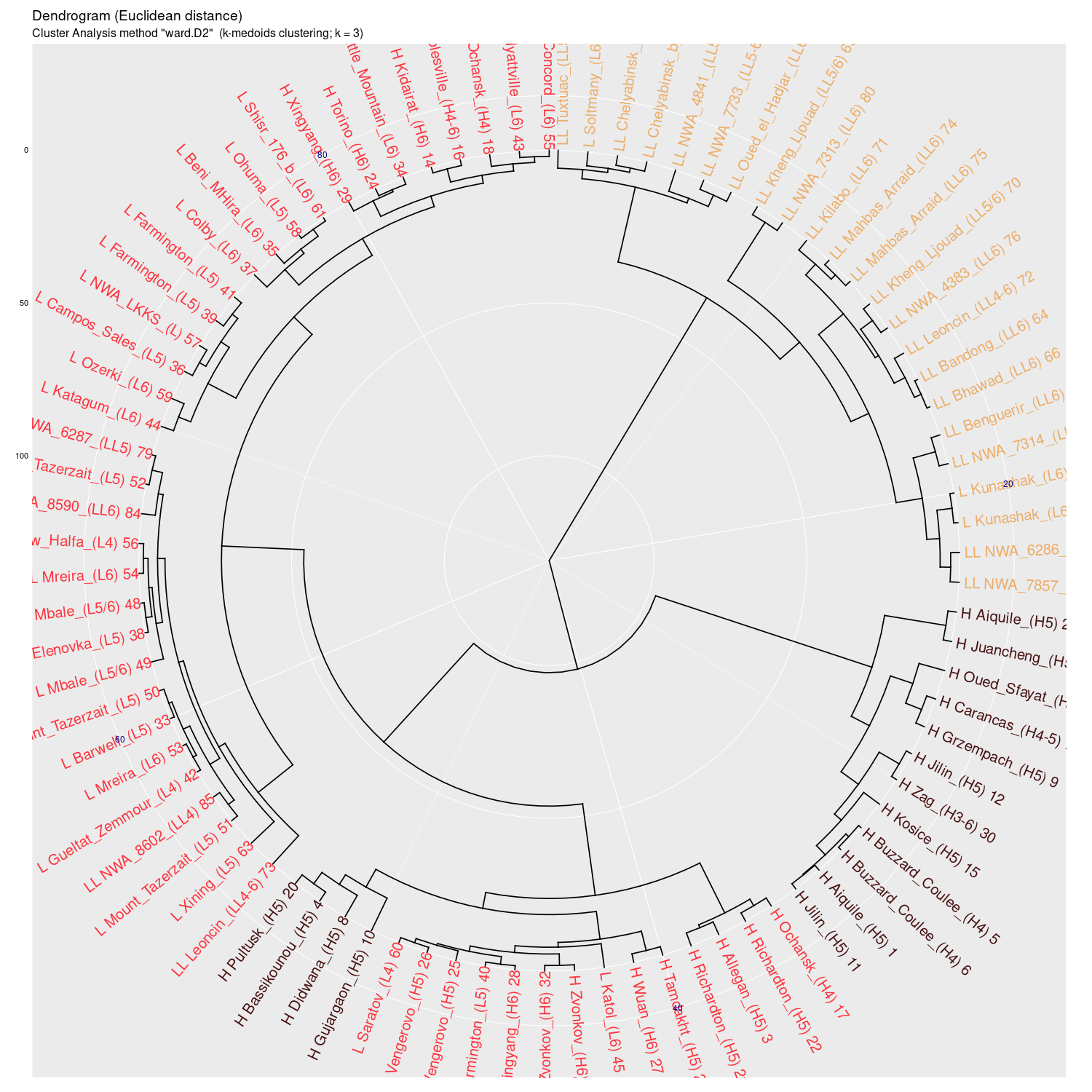
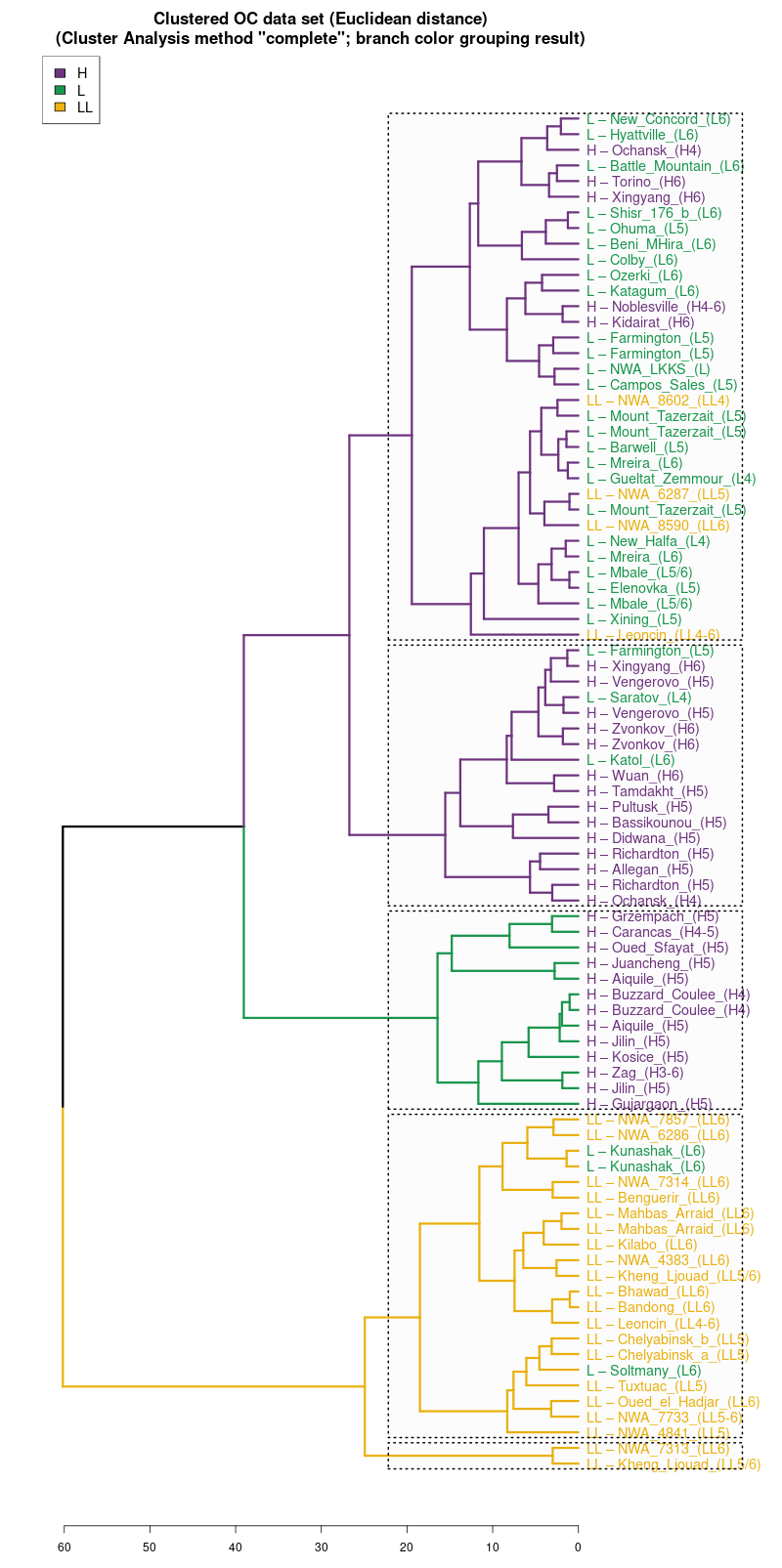
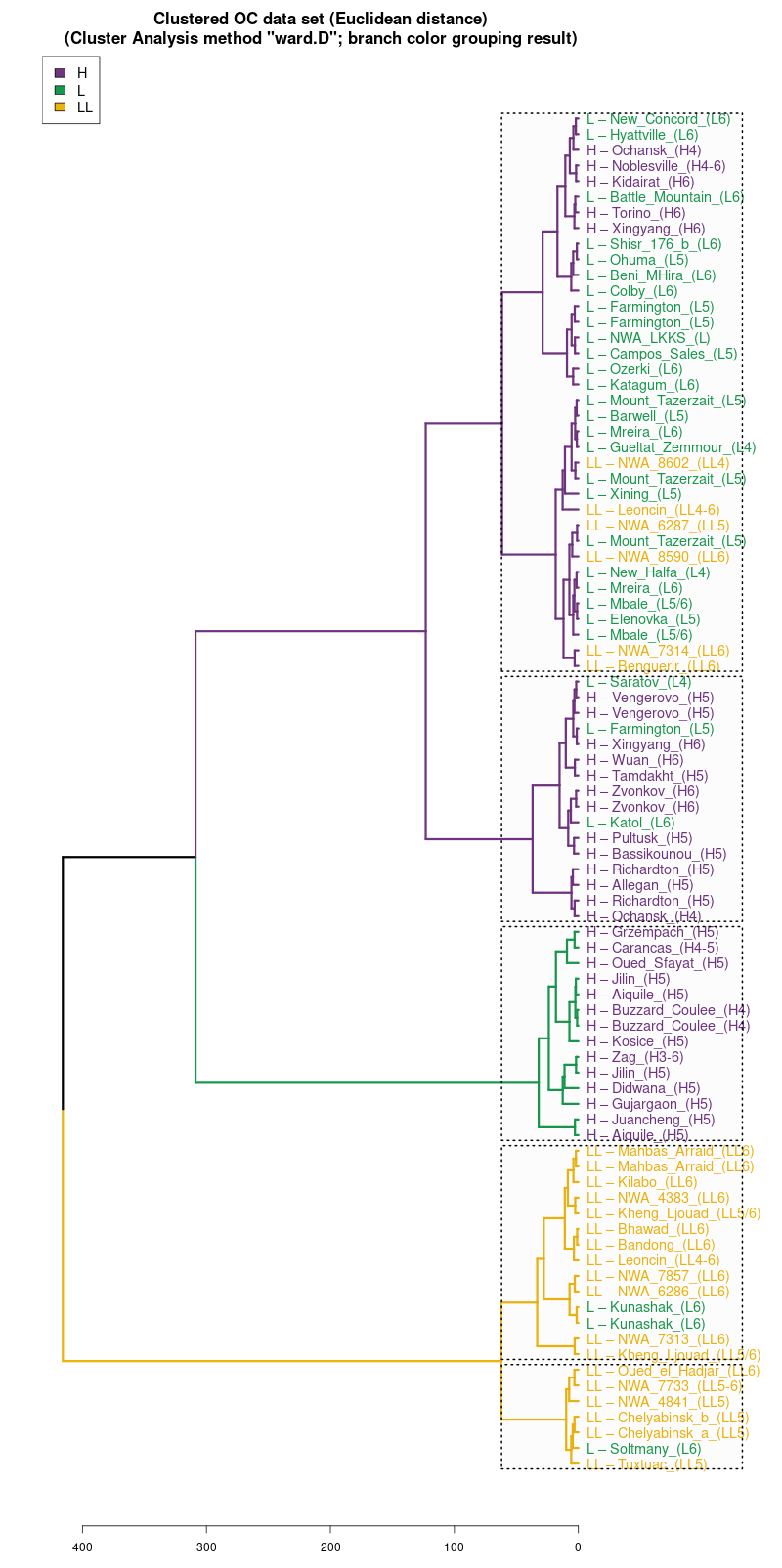
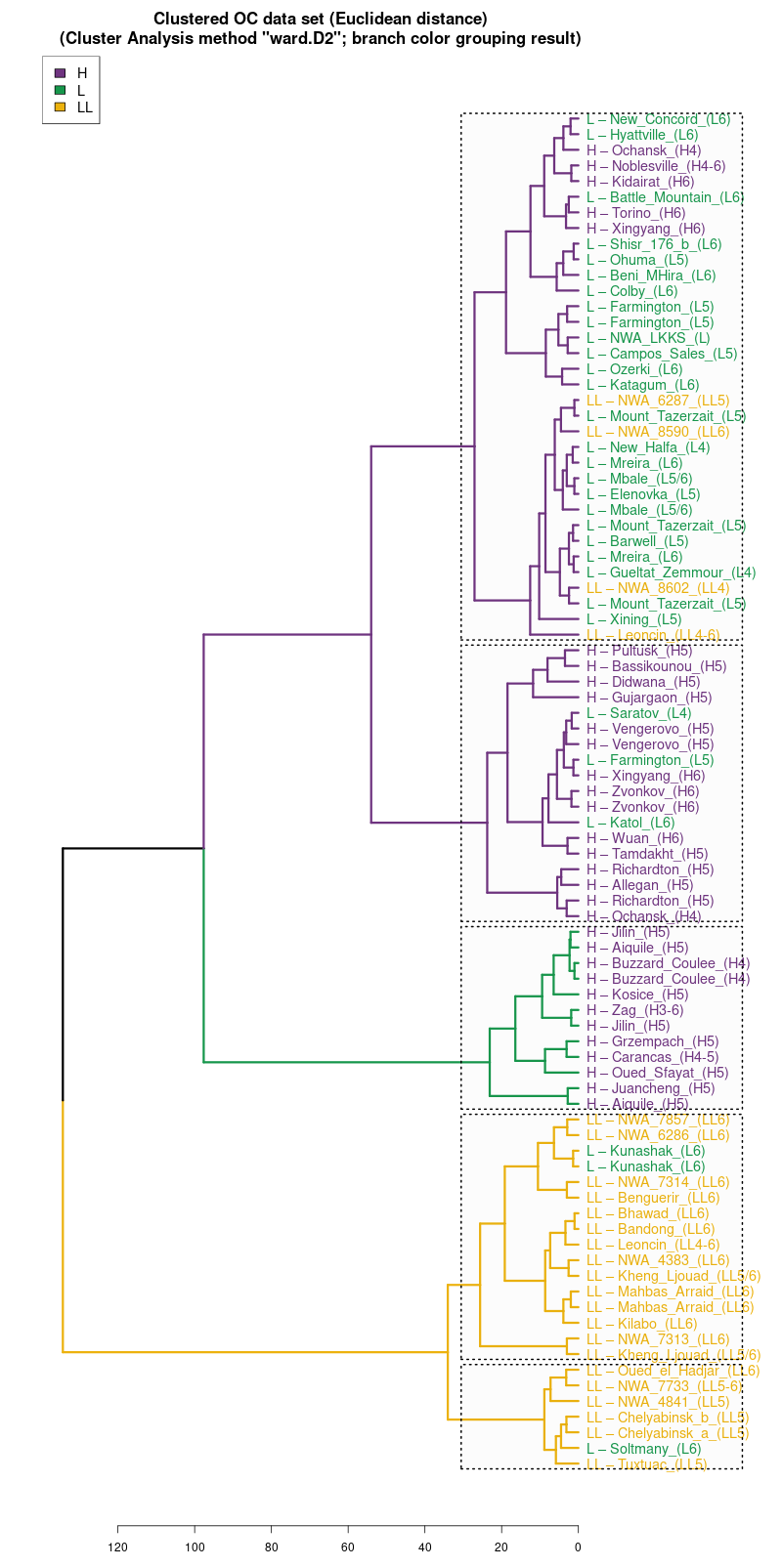
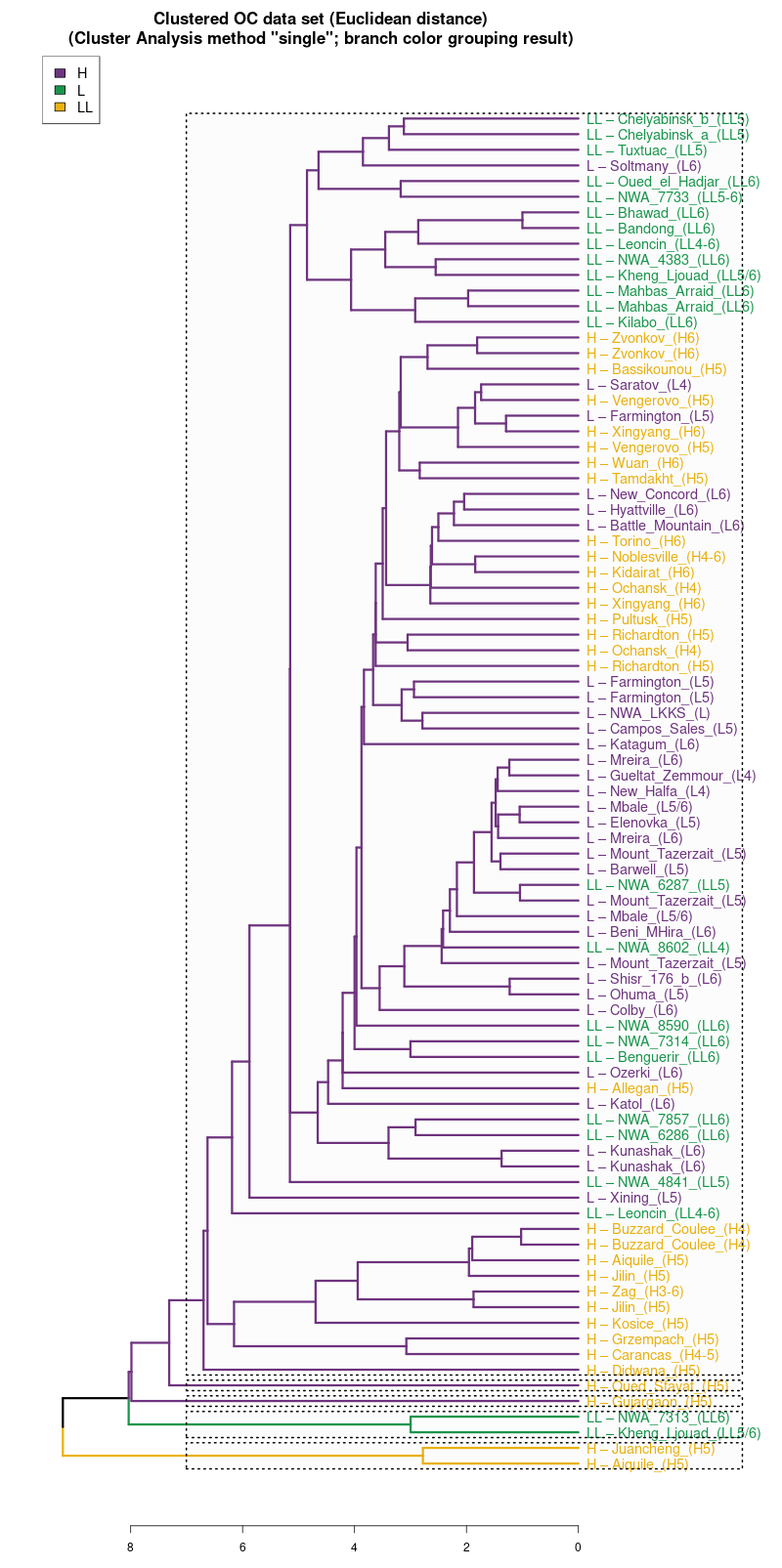
	Analizując trafność (accuracy) metody 4M warto porównać wyniki dla "chybionych" trafień z wynikami analizy skupień. Warto spojrzeć na drzewo klasyfikacyjne w metodzie Ward.D2. Jak część "chybionych" meteorytów jest podobna do nie swoich klas: Katol i Farmington typu L są podobne do typu H; NWA 8590 i NWA 8602 typu LL są podobne do typu L; Kunashak i Sołtmany typu L są podobne do typu LL.
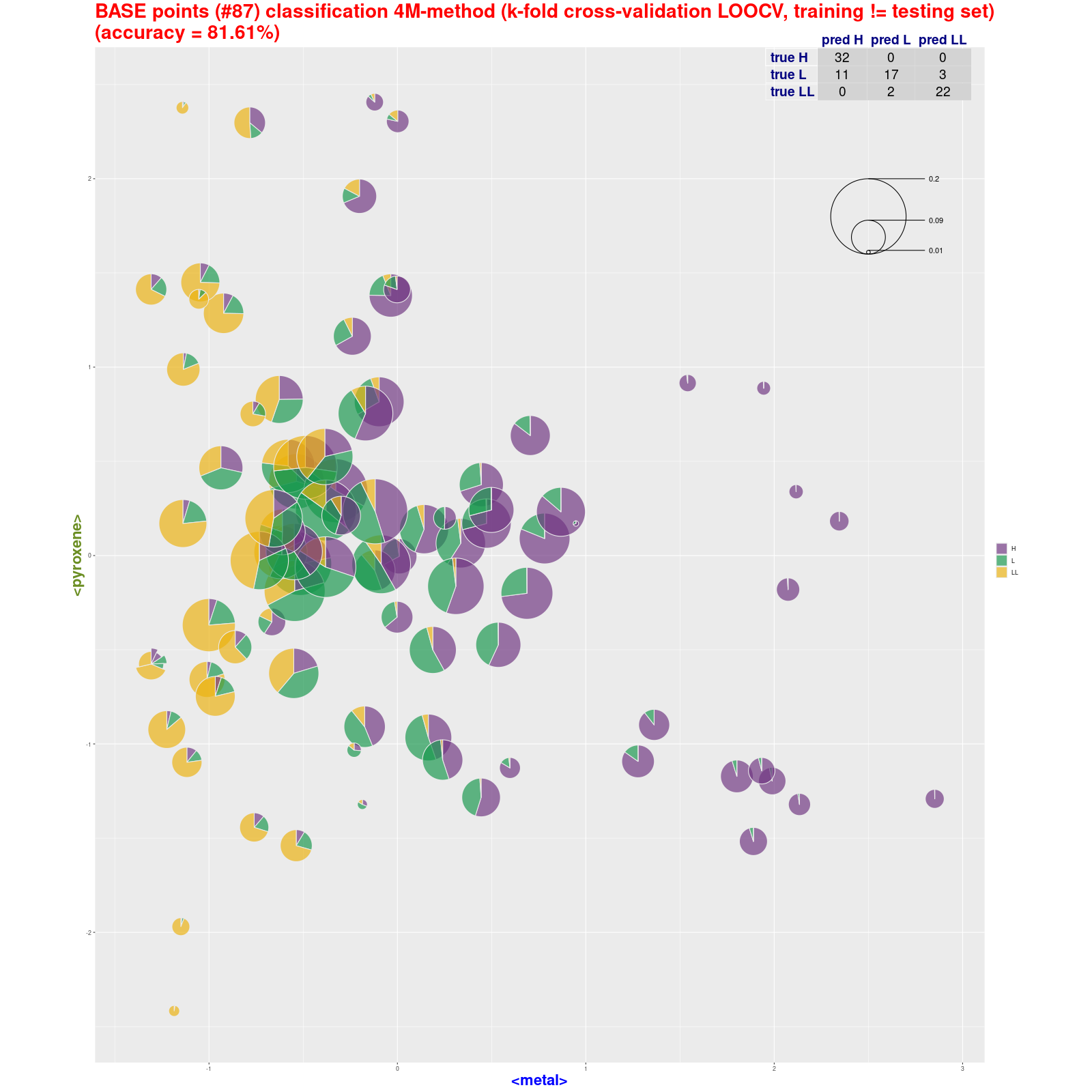
*BASE points classification - 4M-method (pie)* (k-fold cross-validation LOOCV, training ≠ testing set) k-krotny sprawdzian krzyżowy, zbiór testowy ≠ zbiór uczący Rewelacyjna trafność (accuracy) klasyfikacji! Tabela z wynikami klasyfikacji.

BASE points classification - Bayes classification rule (BASE-v2n)

Bayes classification rule (Jajuga 1993).

Obiekt x_i należy do tej klasy j, dla której funkcja:

0.5 * dM_j * dM_j + 0.5 * ln(detS_j) - ln(p_j)

osiąga minimum po j (numer klasy).

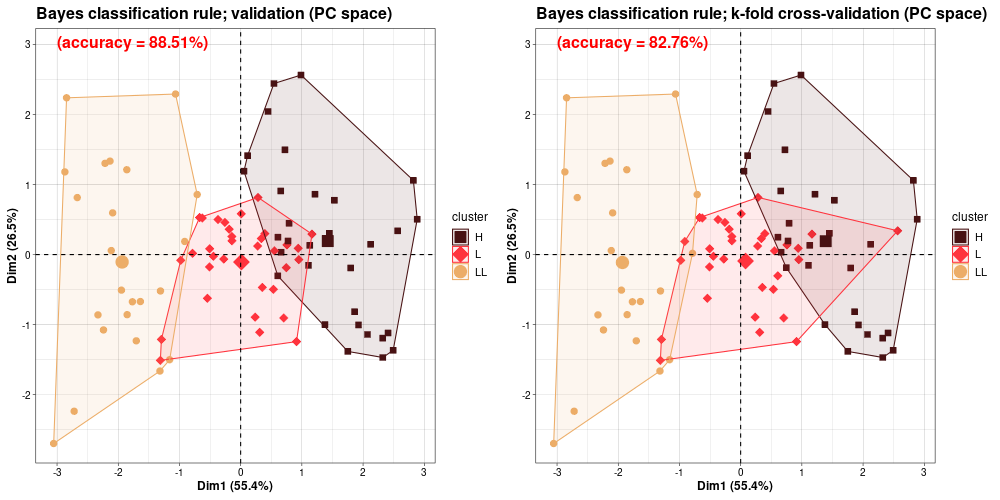
Bayes classification rule in PCA view

...compare

(version HiRes)



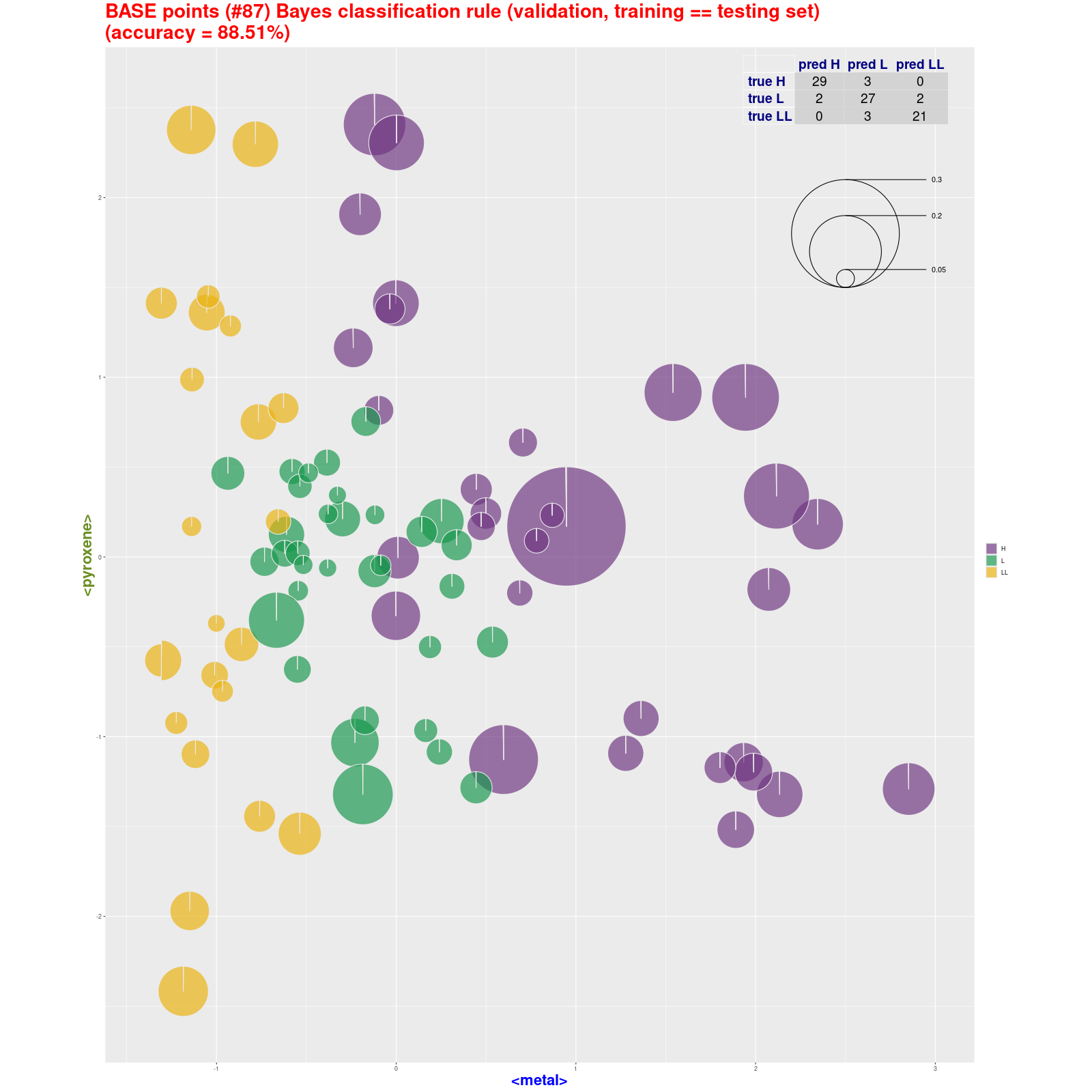
*BASE points classification - Bayes classification rule (pie)* (validation, training ≡ testing set) weryfikacja, zbiór testowy ≡ zbiór uczący Bardzo dobra trafność (accuracy) klasyfikacji! Patrz również → symulacje Tabela z wynikami klasyfikacji.

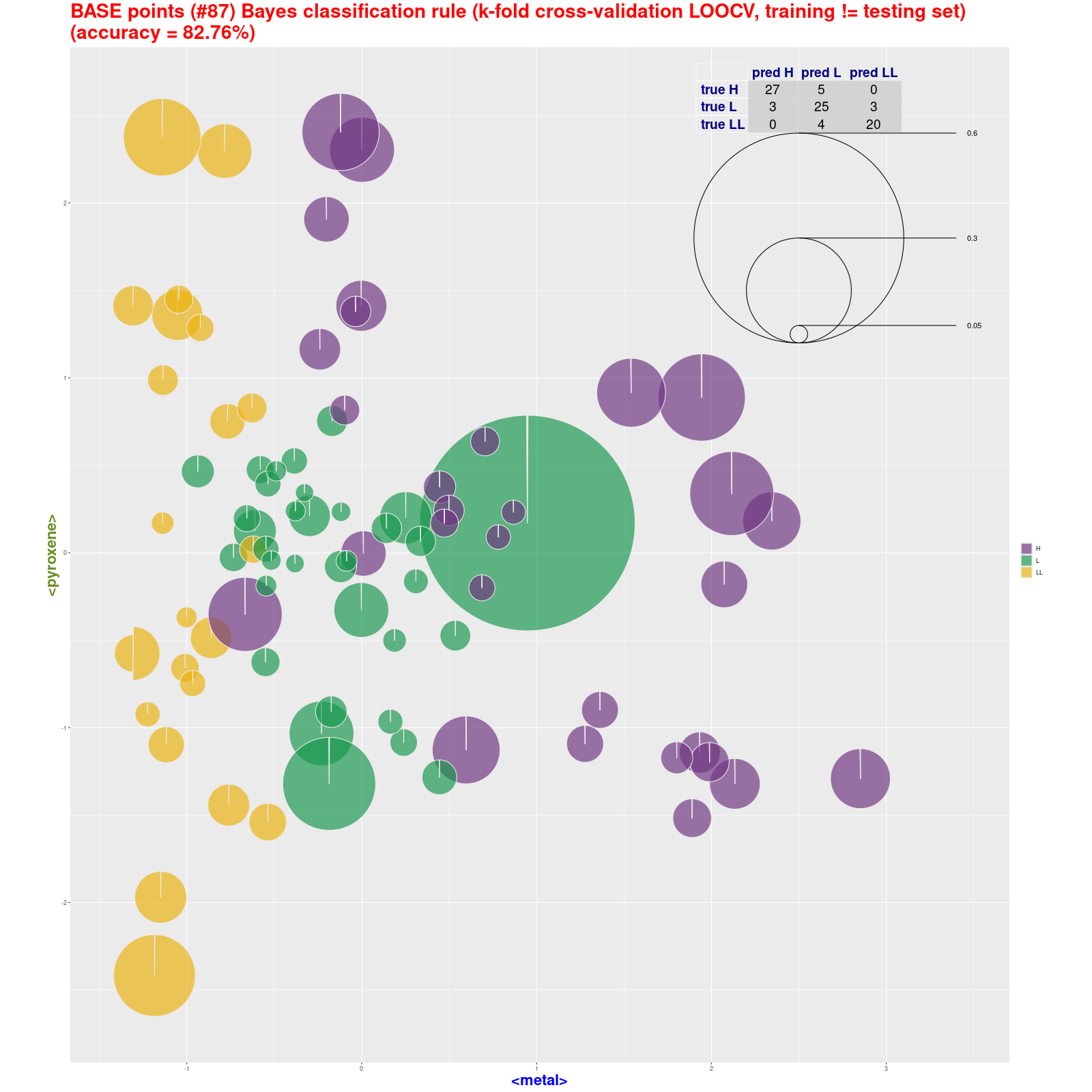
*BASE points classification - Bayes classification rule (pie)* (k-fold cross-validation LOOCV, training ≠ testing set) k-krotny sprawdzian krzyżowy, zbiór testowy ≠ zbiór uczący Bardzo dobra trafność (accuracy) klasyfikacji! Tabela z wynikami klasyfikacji.

Symulacje (BASE-v2n)

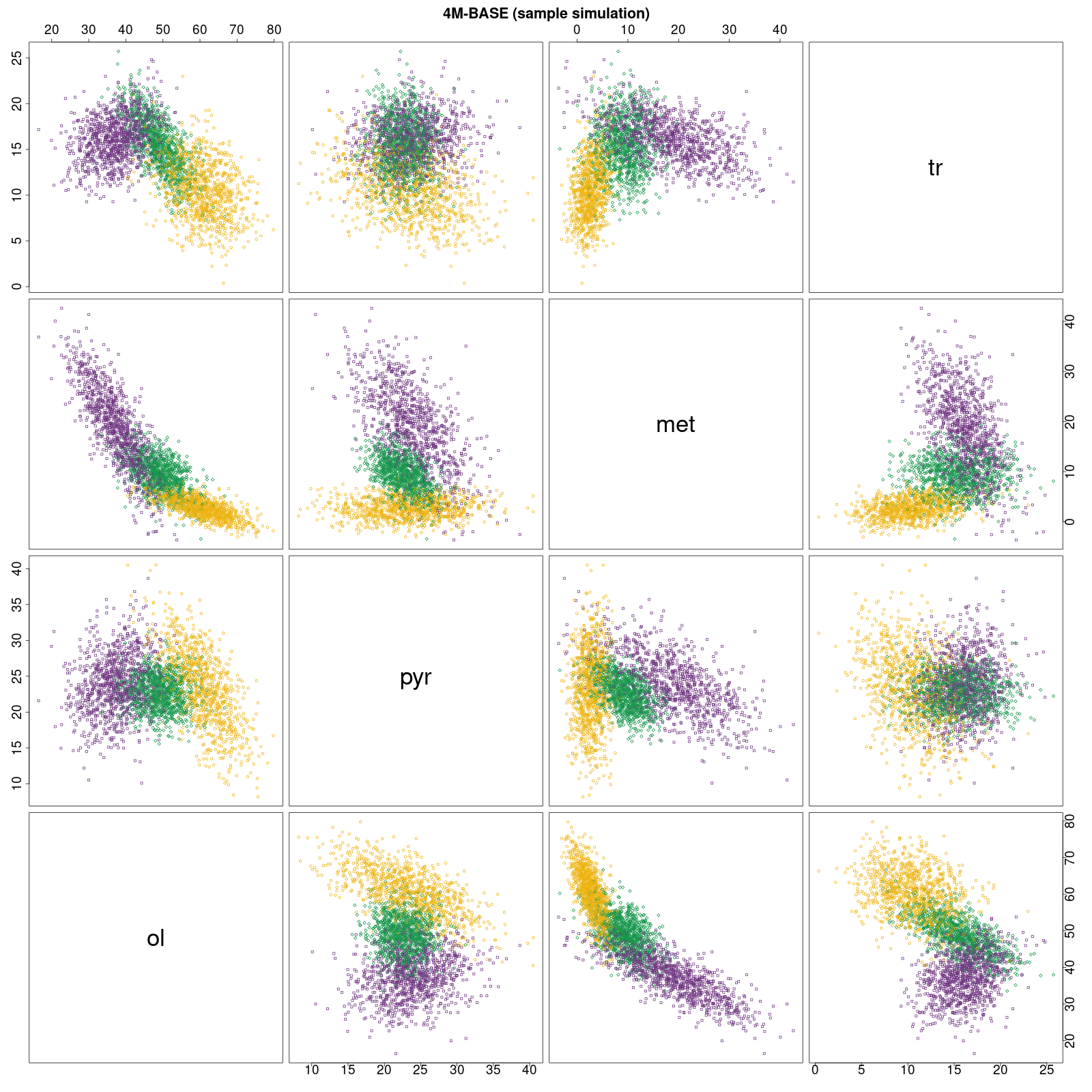
set BASE - simulation (Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

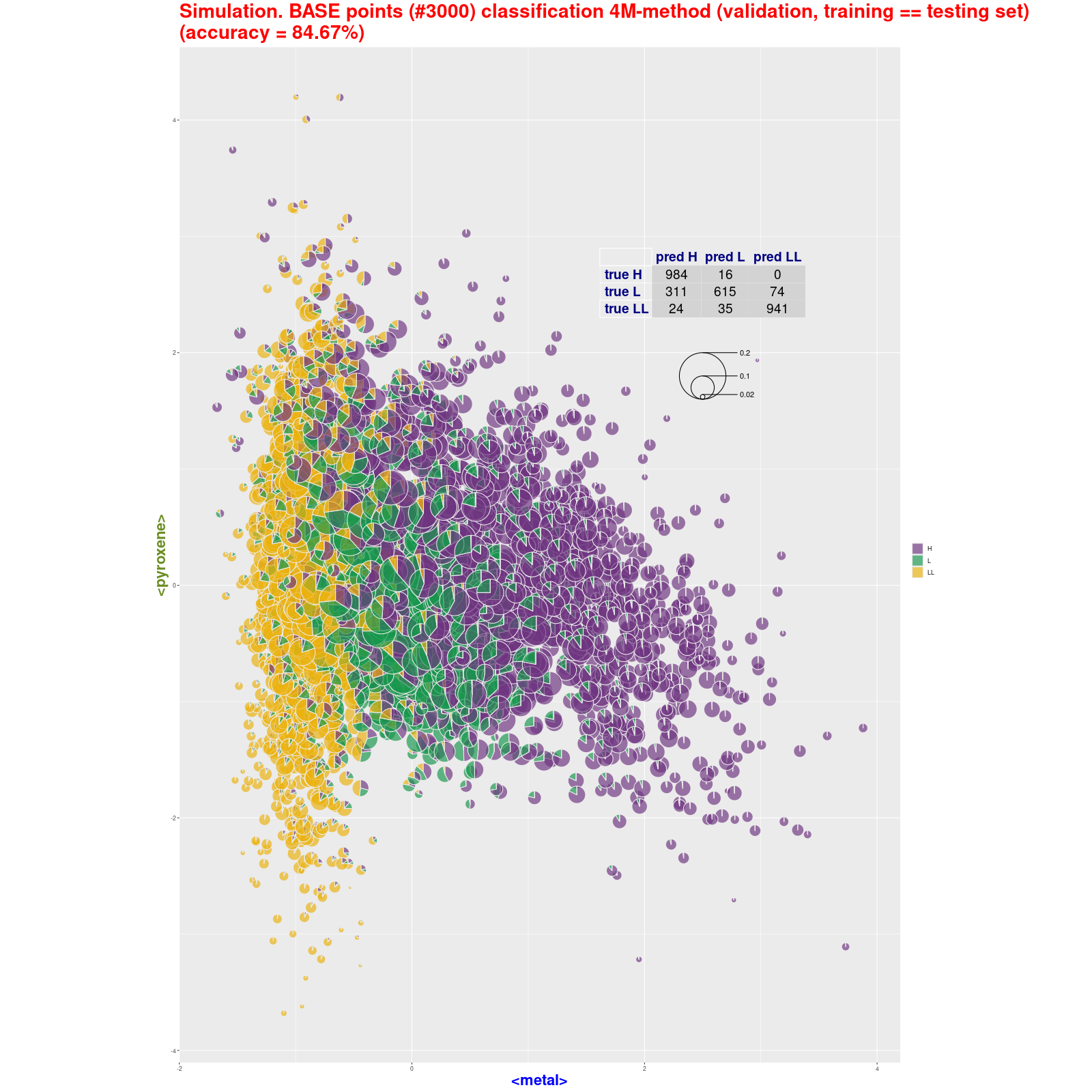
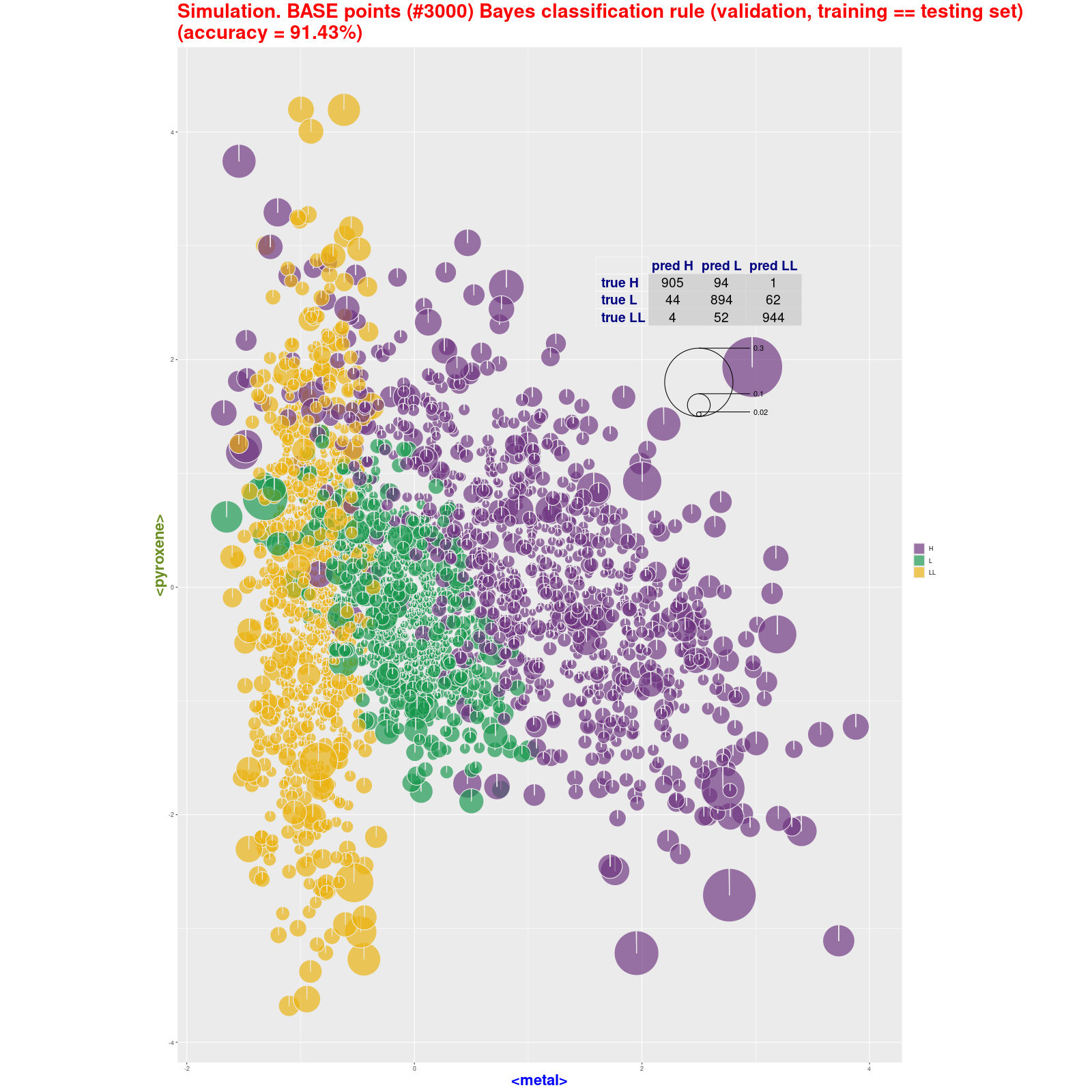
set BASE - BASE points classification (pie)

Symulacja BAZY dla 3×1000 próbek ; symulacja przy zadanych wartościach średnich i macierzach kowariancji

Symulacje testowych baz (losowe zbiory 1000 próbek dla każdego typu) klasyfikowane metodą 4M dawały wynik trafności (accuracy) w przedziale 88-92%; klasyfikowane Bayes classification rule dawały wynik trafności (accuracy) w przedziale >??%
(wykres sporządzony w pakiecie statystycznym R)

Patrz → BASE point classification (pie): 4M method • Bayes classification rule

Tabele z wynikami klasyfikacji: 4M method • Bayes classification rule

Cluster analysis (BASE-v2n)

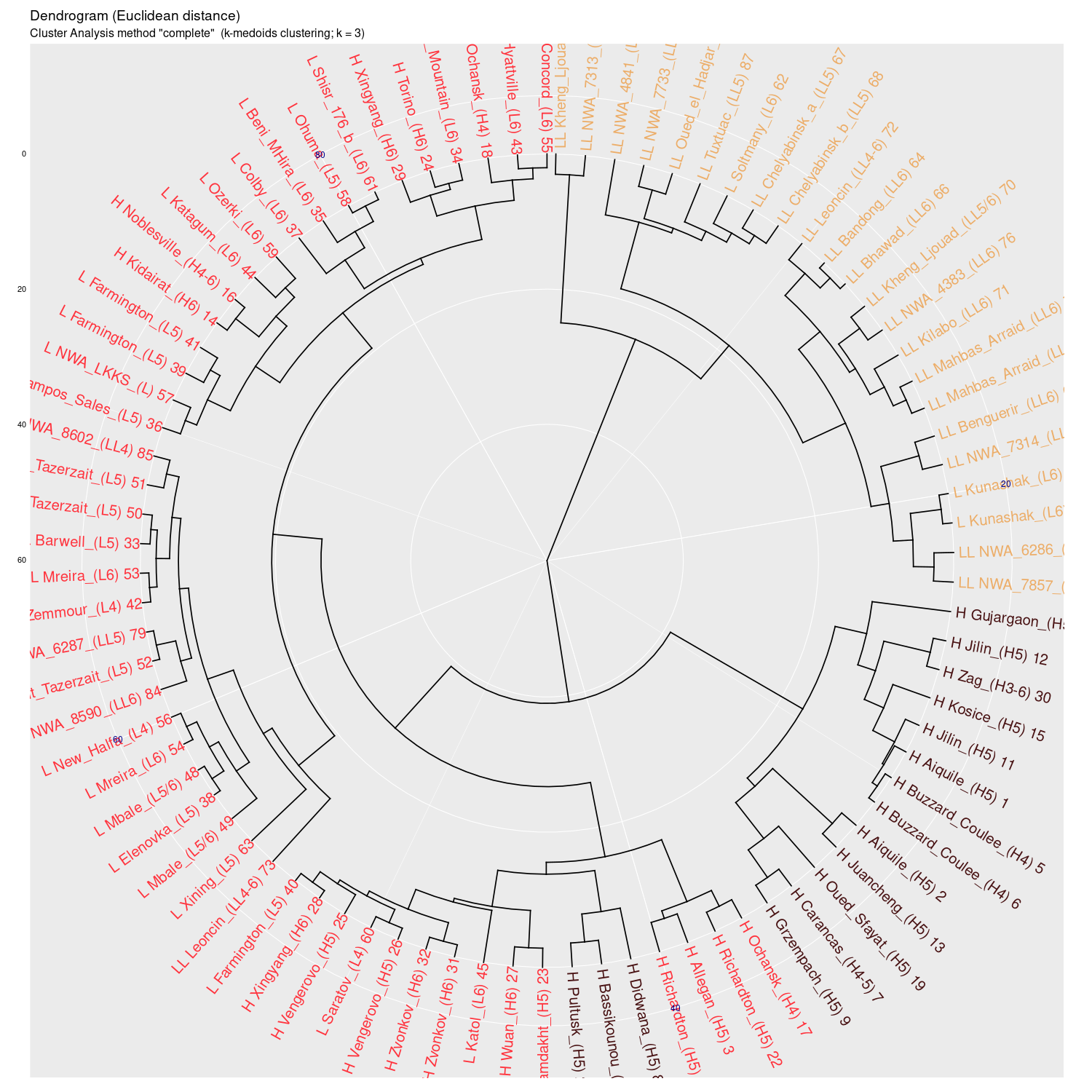
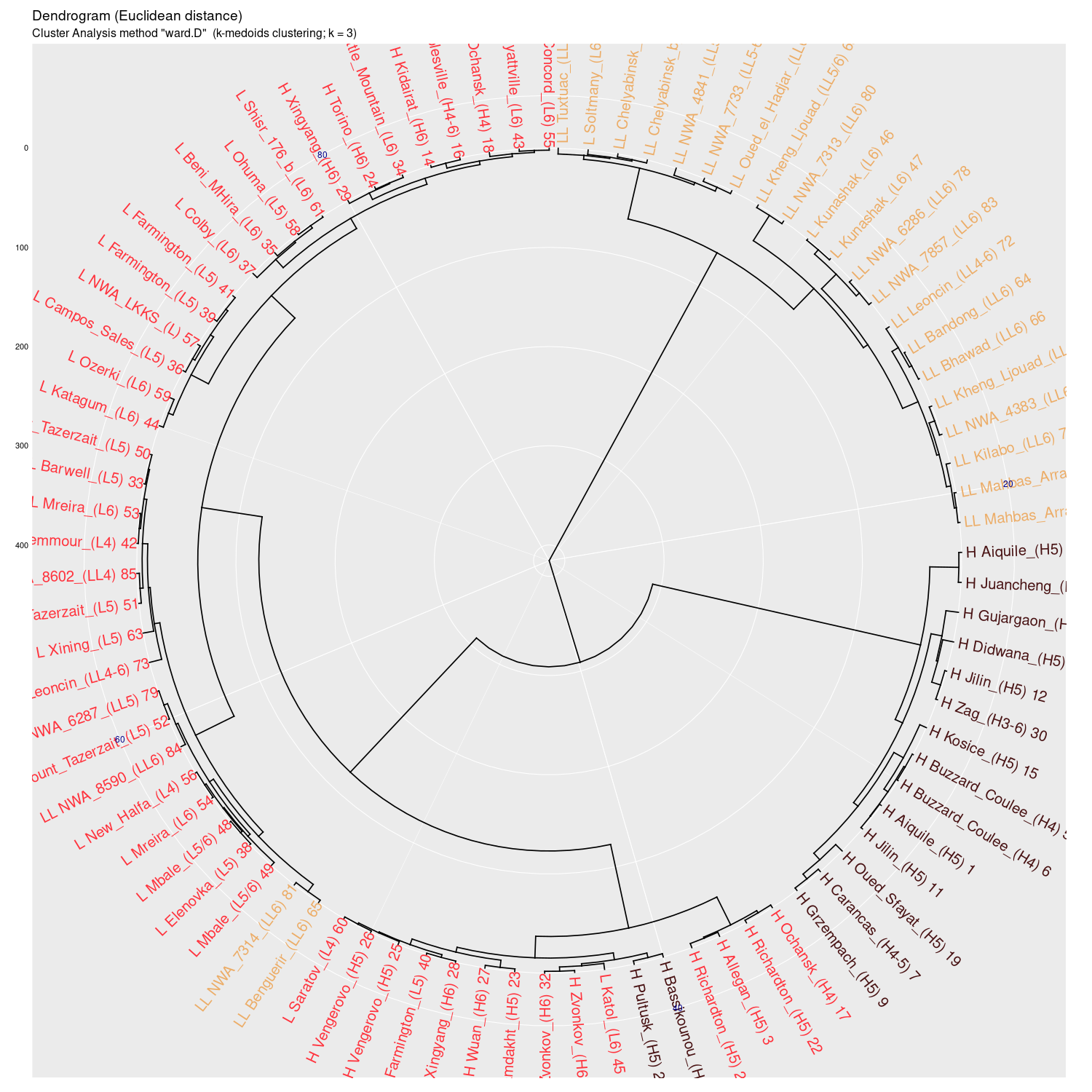
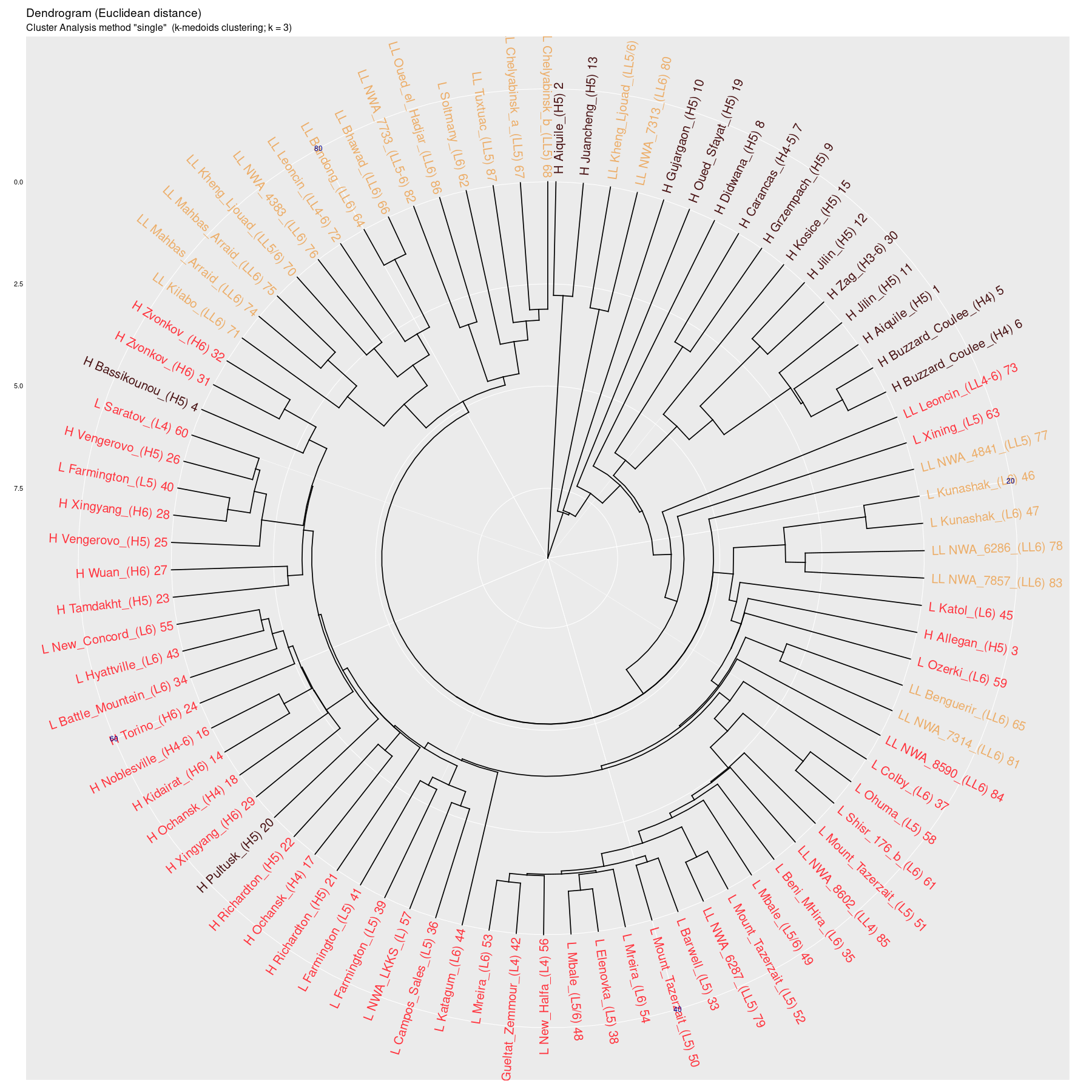
complete	Ward.D	Ward.D2 (see → PIE)	single
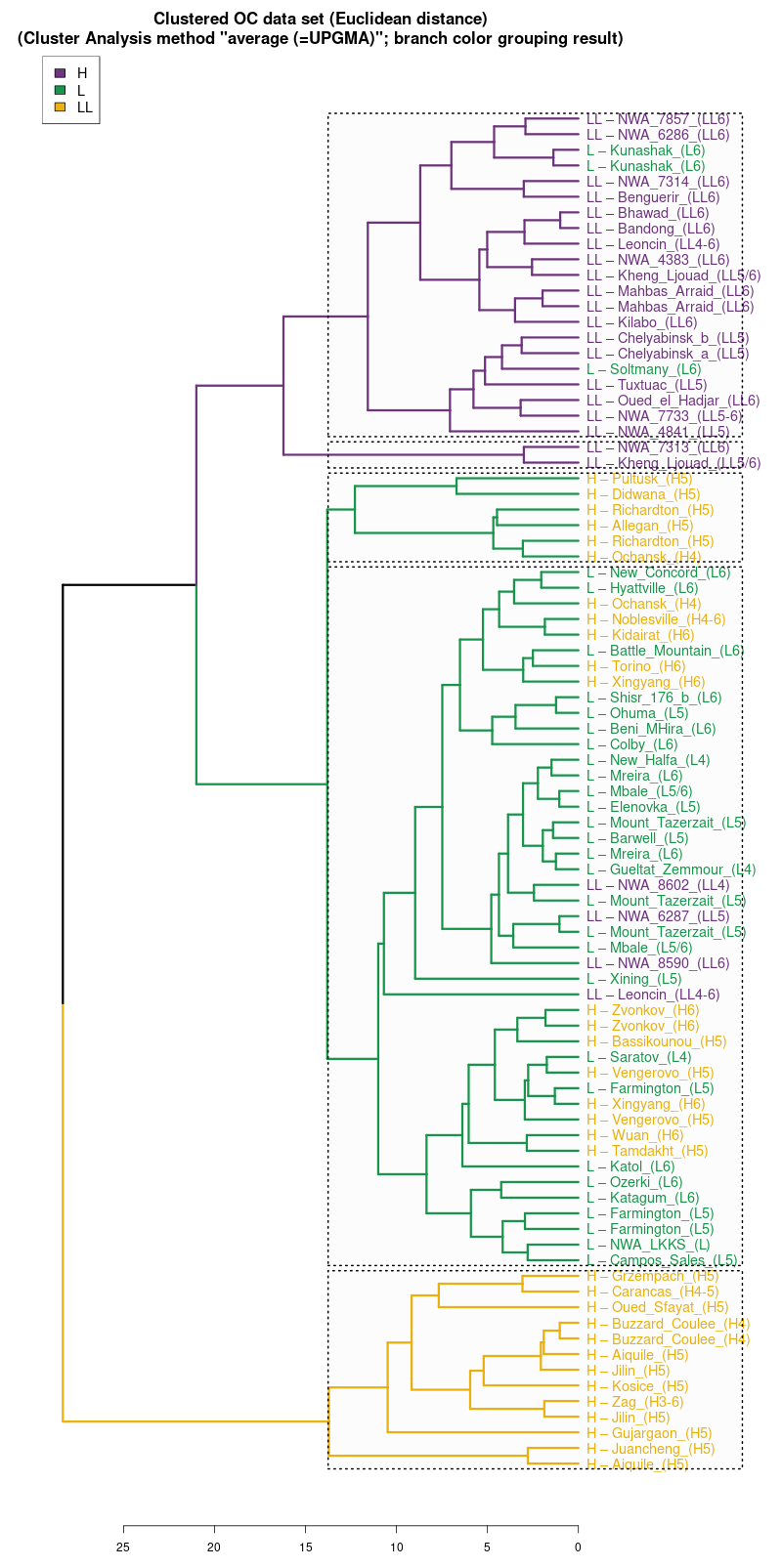
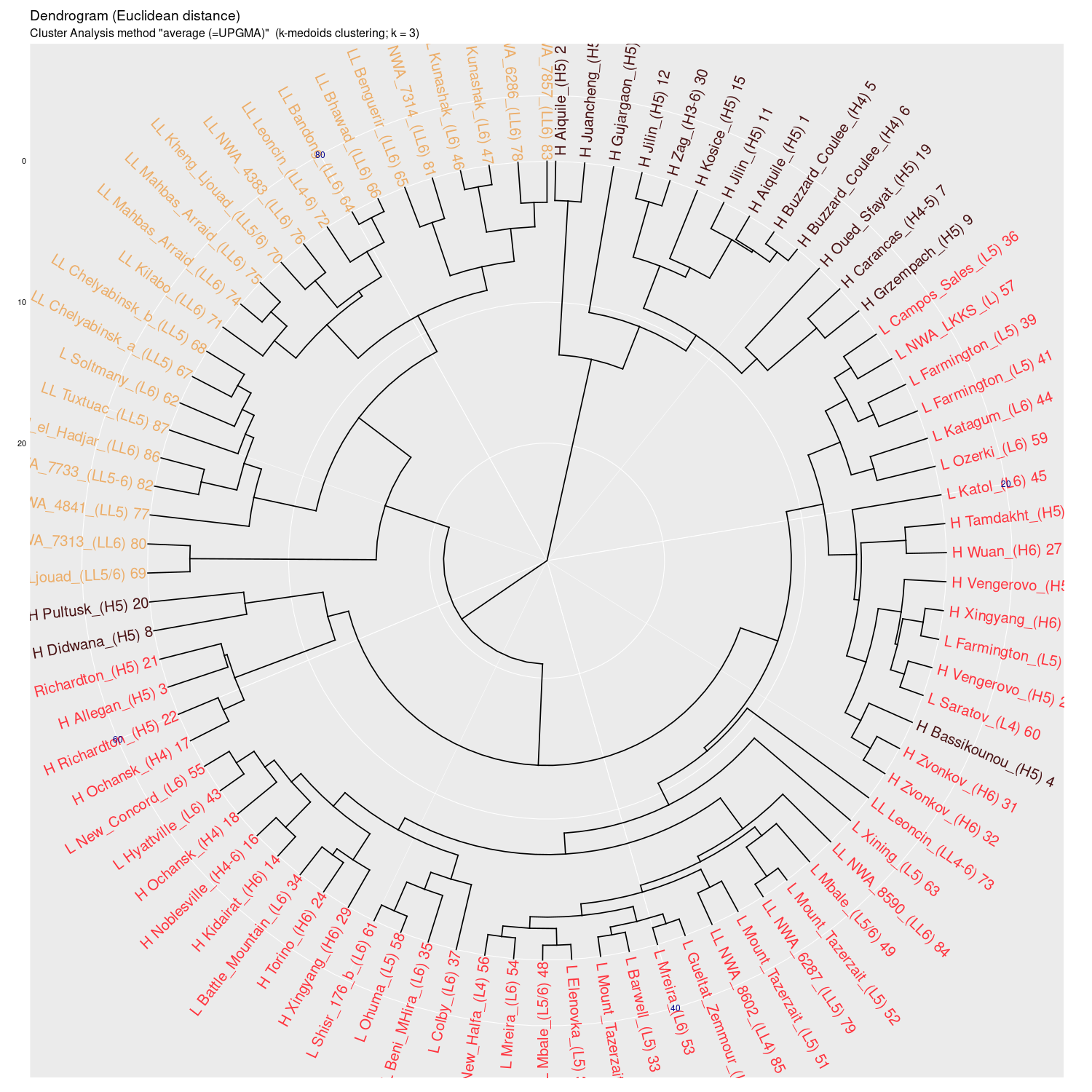
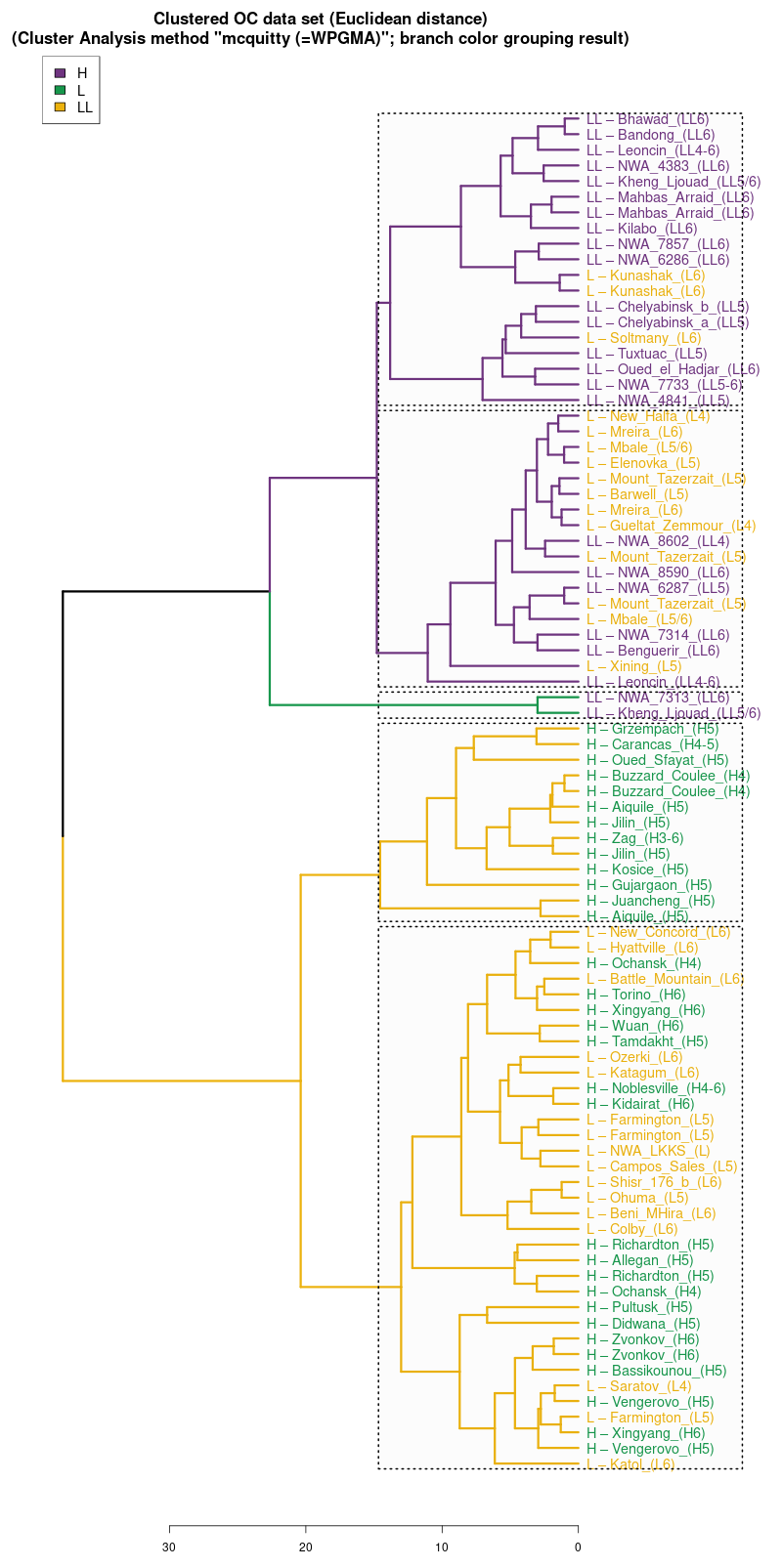
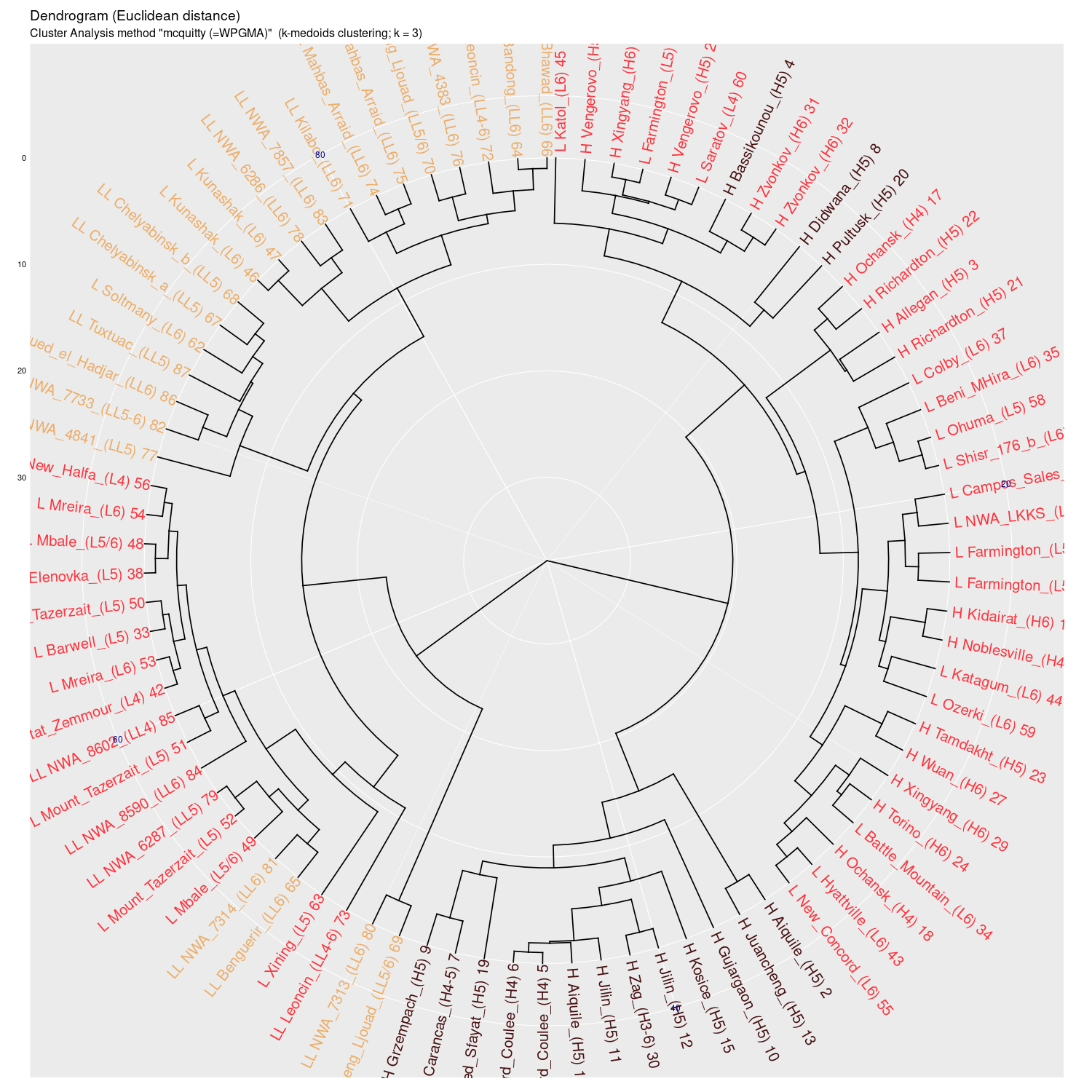
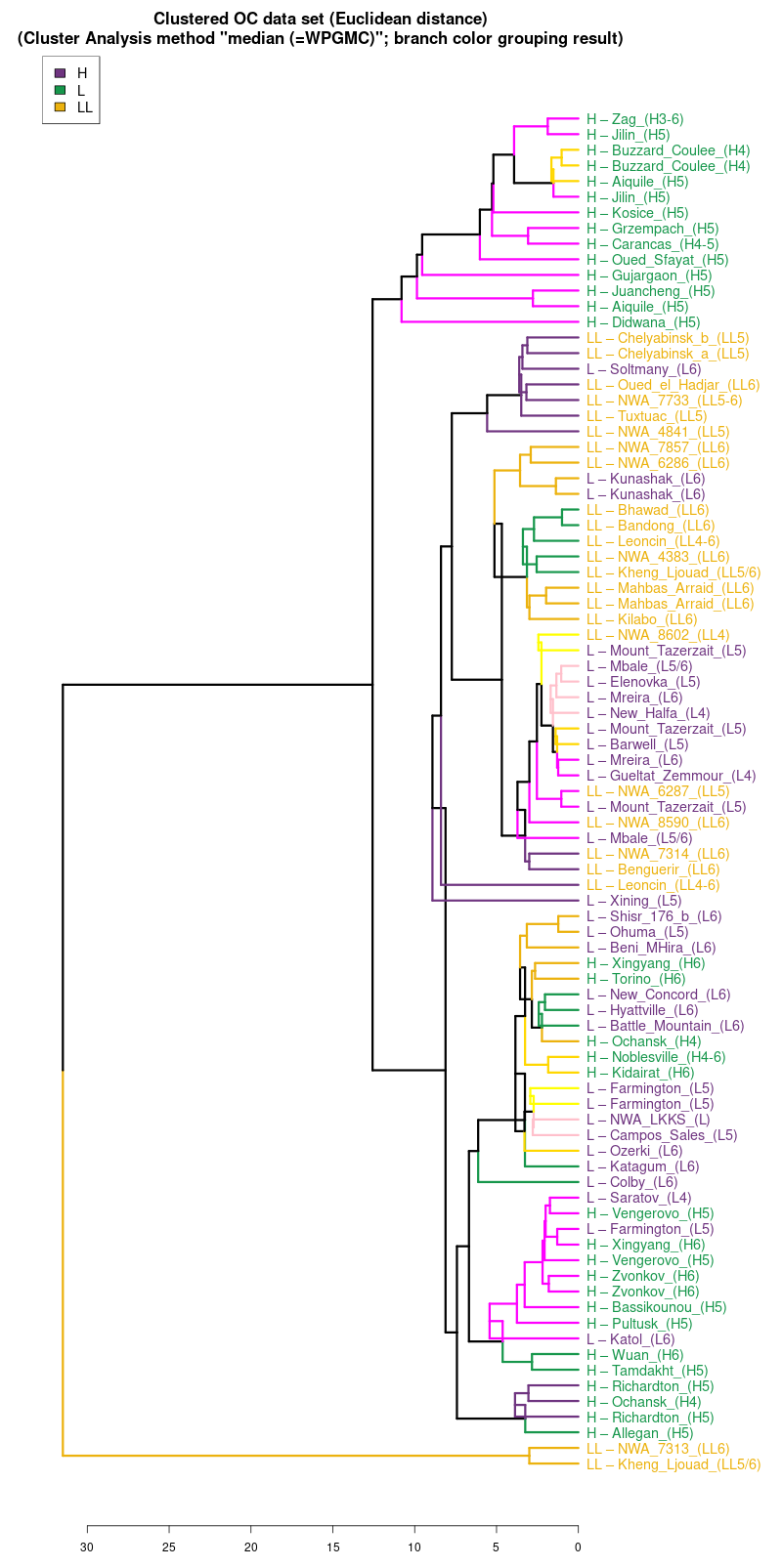
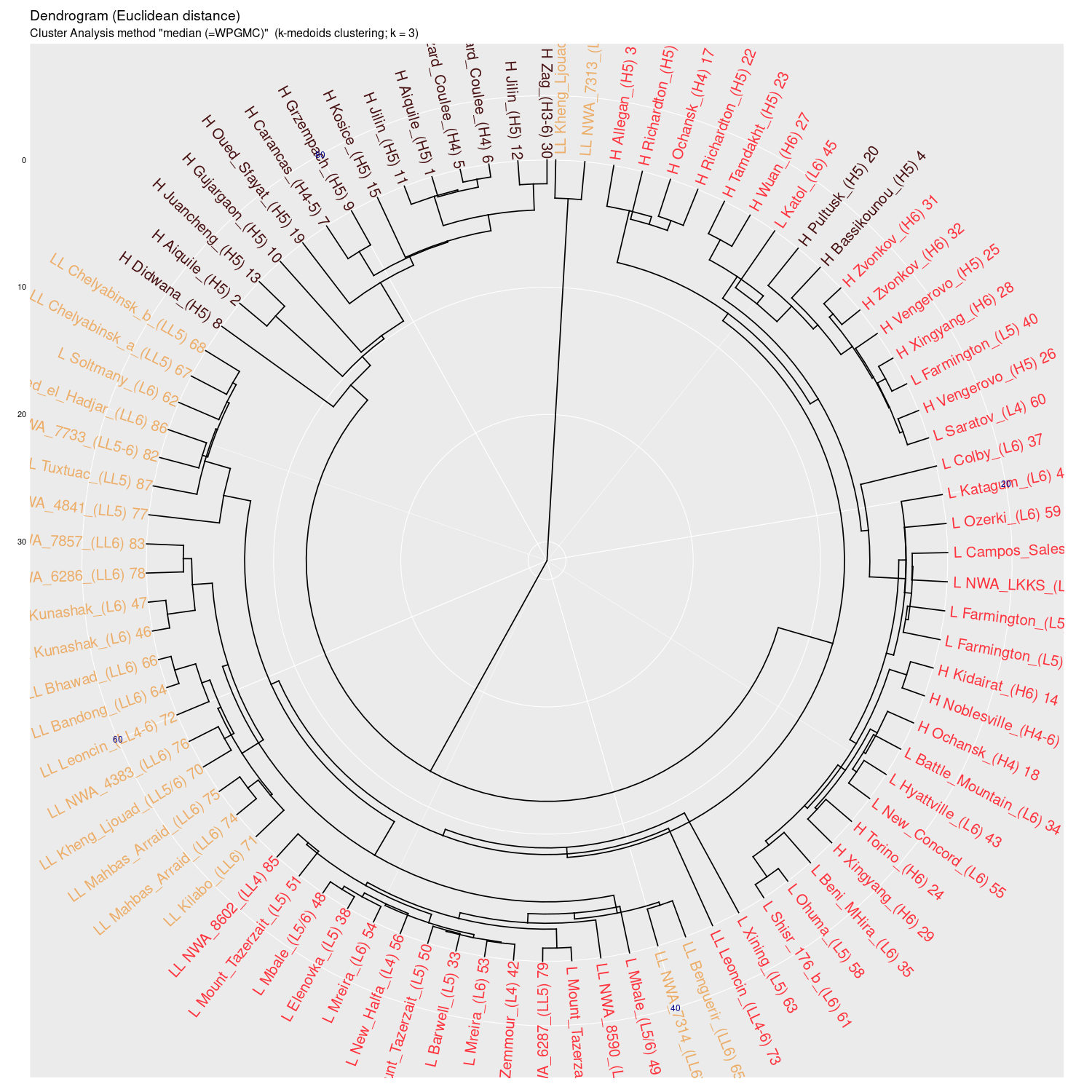
	average (UPGMA)	mcquitty (WPGMA)	median (WPGMC)
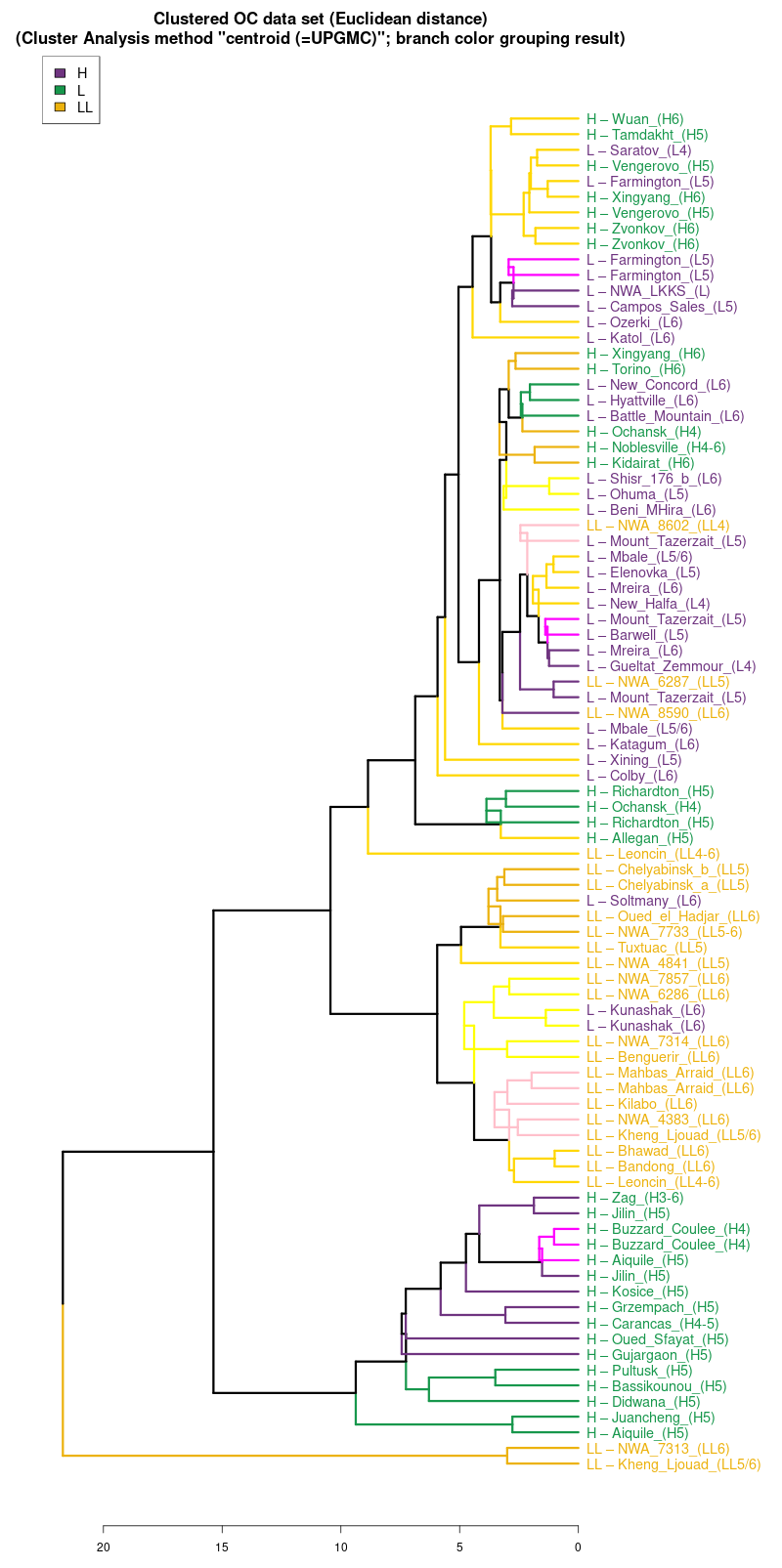
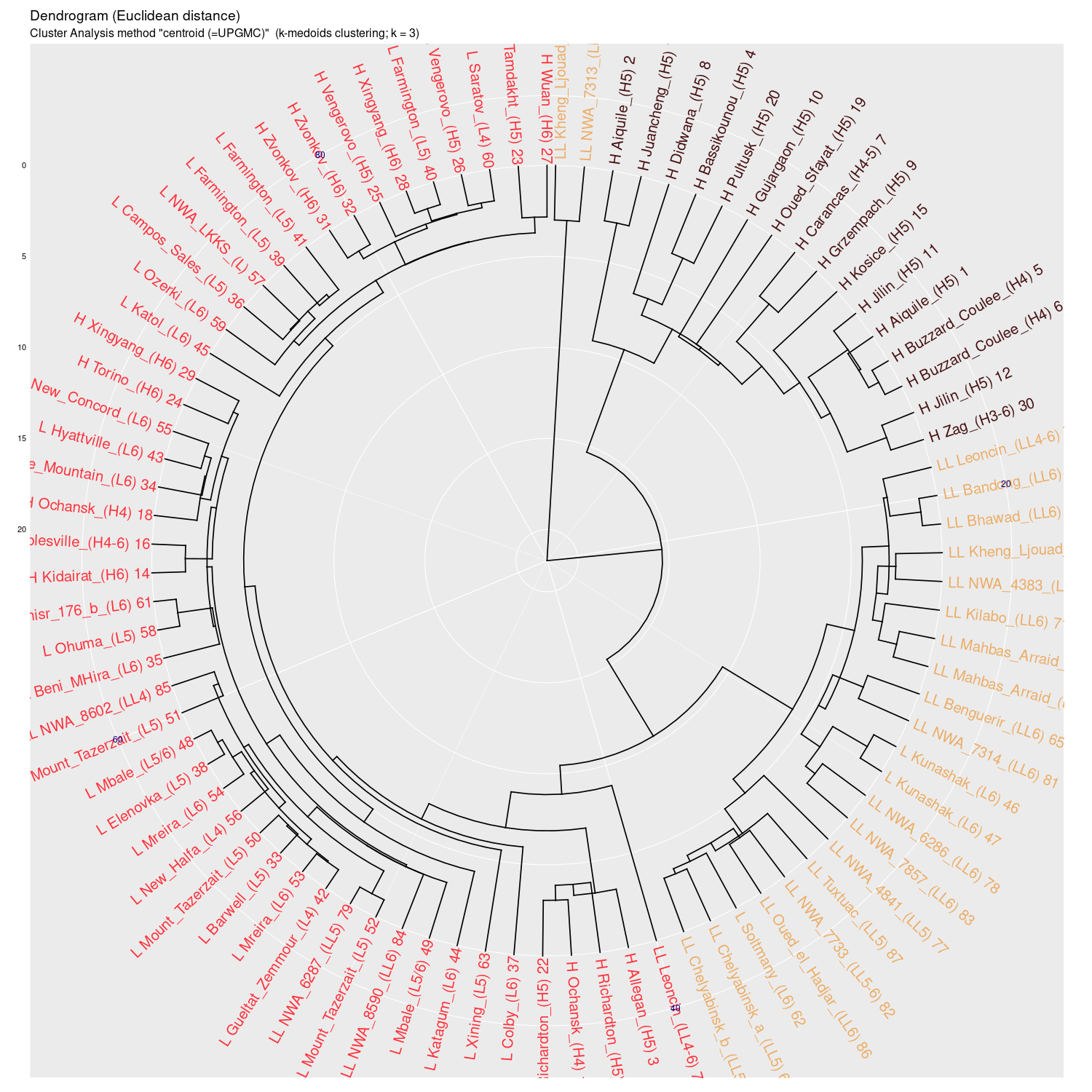
	centroid (UPGMC)

Wykres aglomeracyjny (cluster analysis) na którym widać potencjał dyskryminacyjny parametrów mössbauerowskich (różne metody aglomeracji)
(wykres sporządzony w pakiecie statystycznym R)

complete	Ward.D	Ward.D2	single
	average (UPGMA)	mcquitty (WPGMA)	median (WPGMC)
	centroid (UPGMC)

Wykres aglomeracyjny (cluster analysis + k-medoids)

See → BASE points classification - k-medoids clustering

Testy na IRIS (bottom-right)!

Sources

Woźniak Marek, Gałązka-Friedman Jolanta, Duda Przemysław, Jakubowska Martyna, Rzepecka Patrycja, Karwowski Łukasz, (2019), Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites, Meteoritics & Planetary Science, vol. 54(8), 2019, s. 1828-1839. Plik doi; streszczenie.