Metoda 4M – formularz

Za pomocą załączonego formularza (uwaga: strona otwiera się w osobnym okienku) można obliczyć metodą 4M odległości Mahalanobisa (d_M) oraz poziomy podobieństwa (S_cluster) dla nieznanego meteorytu. Czyli dokonać klasyfikacji – jakiego jest on typu – H, L czy LL?!

Meteoryt przyporządkowujemy do tego typu dla którego wartość poziomu podobieństwa jest największa!

4M-BASE-v2n – najnowsza wersja (ilustracje)

W dalszej części opisano ideę metody 4M.  Nie będzie tam nic o samym zjawisku Mössbauera i spektroskopii mössbauerowskiej, tylko samo gęste. Więc bez wektorów, macierzy i całek, się nie obędzie. Sorry
Tekst dla dociekliwych i wytrwałych

Zastosowanie spektroskopii mössbauerowskiej, wielowymiarowej analizy dyskryminacyjnej i odległości Mahalanobisa do klasyfikacji zrównoważonych chondrytów zwyczajnych
(Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites)

Wielowymiarowa analiza dyskryminacyjna i odległość Mahalanobisa – metoda 4M
(Multidimensional discriminant analysis and Mahalanobis distance—4M method (meteorites-Mössbauer-multidimensional-Mahalanobis))

Wykres zawartość ferrosilitu (Fs) w orto­piroksenach vs. zawartości fajalitu (Fa) w oliwinach w zrównoważonych chondry­tach zwyczajnych dla ponad 5000 ch. zw., dla których podano wartości Fa i Fs w bazie Koblitz Metbase [Koblitz Metbase].

Zaznaczono również wyniki analiz dla meteorytu Goronyo

Wspólnie z fizykami z pracowni spektroskopii mössbauerowskiej Politechniki Warszawskiej oraz geologiem prof. Łukaszem Karwowskim z Uniwersytetu Śląskiego prowadziliśmy pomiary widm mössbauerowskich mało zwietrzałych chondrytów zwyczajnych. Celem naszych badań było sprawdzenie czy wartości powierzchni spektralnych widm mössbauerowskich otrzymane dla różnych chondrytów zwyczajnych mają właściwości dyskryminacyjne? Podobnie, jak te stosowane w klasycznej klasyfikacji mineralogicznej opartej na zawartości fajalitu (Fa) i ferrosilitu (Fs), która jest obecnie podstawową metodą klasyfikacji chondrytów zwyczajnych [Mason 1962; Fredriksson i Keil 1964] (patrz → ilustracja).

  Celem naszych badań było pytanie czy będziemy w stanie określić typ do którego należy badany zrównoważony chondryt zwyczajny tylko na podstawie powierzchni spektralnych jego widma mössbauerowskiego?

  Analizując dane uzyskane za pomocą spektroskopii mössbauerowskiej (patrz → Tabele), staraliśmy się określić typ zrównoważonego chondrytu zwyczajnego w oparciu o liczbowe wielkości powierzchni spektralnych widm mössbauerowskich. Bazując na wcześniejszych ja­ko­ścio­wych badaniach innych zespołów zagranicznych zaproponowałem (opierając się na swoich wieloletnich doświadczeniach z analizą skupień i fascynacji odległością Mahalanobisa) zastosowanie analizy dyskryminacyjnej (multidimensional discriminant analysis), jako właści­wego, ilościowego narzędzia do klasyfikacji [Morrison 1990; Krzanowski 2000].

Nasz model (nasza → baza 4M-BASE) składa się z trzech klastrów (odpowiadających trzem typom zrównoważonych chondrytów zwyczajnych: H, L i LL). Każdy z klastrów (cluster) to zbiór kilkudziesięciu próbek meteorytów danego typu opisanych zestawem czterech wartości (pod)widm mössbauerowskich (każdy pomiar to 4-wymiarowa zmienna (wektor) x = [ol, pyr, met, tr]). Mierzą one cztery podstawowe fazy mineralne z których składają się chondryty zwyczajne – fazę krzemianową (oliwin, pirokseny), fazę metaliczną (kamacyt plus taenit) oraz fazę siarczkową (troilit plus pirotyn).

  Wszystkie wartości parametrów (x) mają tę samą jednostkę (%), ale ich zakresy dla poszczególnych typów są różne. Również wyraźnie widać (patrz → rysunki), że parametry te są ze sobą skorelowane. Wyliczone wartości korelacji przedstawione w → tabelach potwierdzają to spostrzeżenie.

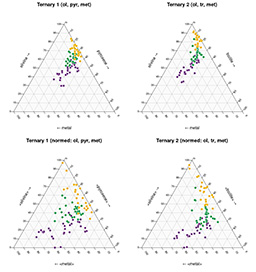
Wykres trójkątny (ternary plot) na którym doskonale widać potencjał dyskrymina­cyj­ny parametrów mössbau­erow­skich

Dysponując 4-wymiarową (4D) przestrzenią parametrów möss­bau­erow­skich (x) chcieliśmy w sposób obiektywny i ilościo­wy określić, jak „daleko” leży nasz badany punkt (chondryt zwyczajny o nie­znanym typie) od zdefinio­wanych klastrów (typów H, L i LL)?  Innymi słowy dokonać klasyfikacji badanego meteorytu!

  Ze względu na istniejące korelacje między wartościami powierzchni spektralnych widm mössbau­erow­skich, odległość euklidesowa nie jest właściwą metryką do określania odległości między punktem reprezentu­jącym nasz nie­sklasyfikowany meteoryt, a klastrami w naszym modelu. Zapropono­wałem zastosowanie właściwej w takich zagadnieniach metry­ki (mojego konika ) – odległości Mahalanobisa, która określa odległość między dwoma punk­ta­mi w przestrzeni n-wy­mia­rowej oraz różnicuje wkład poszcze­gólnych zmiennych i uwzględ­nia korelacje pomiędzy nimi (patrz → Załącznik A).

gdzie:  d_M to odległość Mahalanobisa badanego punktu do centroidu; natomiast s_aver. to „średnia wariancja” wielo­wy­mia­rowego klastra (skupienia, grupy).

4Mb – Bayesowska reguła klasyfikacji (Bayes classification rule)

Wprowadzona przez nas w metodzie 4M miara – poziom podobieństwa (S_clust), ma charakter intuicyjny, więc nie ustawaliśmy w poszukiwaniach innych kryteriów klasyfikacji w oparciu o podobieństwo badanego meteorytu do zbioru pomierzonych i sklasyfikowanych meteorytów (Baza).

  Każda idea klasyfikacji polega na zminimalizowaniu prawdopodobieństwa błędu (funkcja celu) przypisania obserwacji do złej klasy. U nas obserwacja to wektor (x) wartości pól podwidm badanego meteorytu, a klasa to zbiór pomiarów (Baza) chondrytów zwyczajnych definiujących podpopulacje – grupy H, L i LL. Poszukujemy funkcji dyskryminacyjnej, która ma osiągnąć maksimum dla przynależności badanej próbki do danej podpopulacji.

Często stosowaną metodą klasyfikacji jest Bayesowska reguła klasyfikacji (Bayes classification rule). Polega ona na przydzieleniu obserwacji (x) do jednej z k podpopulacji (klasy, klastra π_k), dla której jest spełniony warunek:

        (1)

gdzie: P(π_k|x) – prawdopodobieństwo a posteriori, że obserwacja x należy do podpopulacji π_k. Oblicza się je ze wzoru Bayesa:

        (2)

gdzie p_k – prawdopodobieństwo a priori, że obserwacja x należy do podpopulacji π_k; a f(x|π_k) – to funkcja gęstości rozkładu (warun­kowego) wektora x w podpopulacji π_k; k – ilość podpopulacji;

  Nasz przypadek. Poszczególne podpopulacje (k=3) są opisane 4-wymiarowym rozkładami normalnymi o różnych średnich μ_k i macierzach kowariancji Σ_k. Więc ich funkcje gęstości mają postać:

        (3)

Podstawiając je do równania (2) oraz logarytmując (funkcja monotoniczna i rosnąca) i pomijając elementy stałe, otrzymujemy funkcję quadratic discriminant function (QDF)

        (4)

gdzie: p_k – prawdopodobieństwo a priori, że obserwacja należy do podpopulacji π_k; w naszym przypadku prawdopodobieństwa a priori przynależności badanego chondrytu do jednej z grup wynosi 1/3 (tak też wskazują statystyki spadków i znalezisk chon­drytów zwyczajnych).

  Jak widać funkcja dyskryminacyjna g() zależy od odl. Mahalanobisa, wyznacznika macierzy kowariancji (Σ_k) i prawdo­podo­bieństwa a priori (p_k):

        (5)

Sprawdziliśmy nowe kryterium klasyfikacji - funkcję g() - dla naszej Bazy. Poprawność wyników jest na poziomie >94% (rysunek)!

Nowa metoda/nowe kryterium 4Mb:

4M-BASE-v2n – najnowsza wersja (ilustracje)

The 4M vs. 4Mb method – from the level of similarity to the maximum a posteriori

Figure 1. Graphic presentation of the relative areas (expressed as percentages) of four sub­spectra representing the following types of pha­ses: ol – olivine, pyr – pyroxene, met – metal­lic phase, and tr – troilite, determined for mete­ori­tes constituting the database of the studied and classified ordinary chondrites (sym­bols: purple – group H, green – group L, yellow – group LL).

The idea of the 4M method is based on the observation that the areas of the subspectra representing individual iron-containing phases like olivine, pyroxene, troilite and Fe-Ni alloys, observed in Mössbauer spectra of ordinary chondrites, have discriminatory properties, which allowed us to use them for the assignment of the tested object to specific groups. As illustrated in Figure 1 the percentage share of these phases reveal different ranges of values that are characteristic for each type of ordinary chondrites (H, L and LL).

  We have compiled a database of examined and classified (using the classical method) ordinary chondrites, which consists of a collection of several dozen samples of meteorites belonging to the respective groups (subpopulations H, L and LL). Each of these samples is described by a set of four parameters corres­ponding to the values of the areas of the Mössbauer subspectra representing olivine, pyroxene, metallic phases and the sulfide phase. In the 4-dimensional space of these Mössbauer parameters, in which each point corresponds to one element of the database, meteorites belonging to the same subpopulations form three different, but partially overlapping clusters. We were looking for a method to objectively and quantitatively determine how far a certain point of study (for unclassified ordinary chondrite) is from each centroid of defined clusters of subpopulations H, L and LL. In other words, by comparing these distances we expect to classify the meteorite being tested.

Figure 2. BASE points classification – the 4M-method (pie charts) (validation, training ≡ testing set). The size of each circular graph is pro­portio­nal to the sum of the levels of simi­larity (S_clust). The portions in the pies are pro­portio­nal to the levels of similarity to individual groups. The accuracy table collects the results of the classification of meteorites from different groups ("true") related to recogni­zed/predicted groups ("pred"). The correctness of the classification using the 4M method is about 88%.

  Due to the observed correlations between the area values of the Mössbauer subspectra, the Euclidean distance was not a suitable measure for determining the distance between a selected point, representing an unclassified meteorite, and the clusters in our model. Therefore, we proposed the use of a measure appropriate in such cases – the Mahalanobis distance, which determines the distance between two points in n-dimensional space and differentiates the contribution of individual variables and takes into account the correlations between them. For each un­known meteorite, it is possible to calculate the Mahalanobis distances from the centroids of three clusters and on this basis assign the studied object to the subpopulation (class) to which it is closest, i.e., it corresponds to the smallest Mahalanobis distance.

  Taking into account the fact that individual clusters in 4D space have a complex form, we proposed that the classification criterion should not be the Mahalanobis distance itself, but the quantity, which also considers the shape and volume of the clusters. We introduced a parameter called the level of similarity (S_clust) based on the Mahalanobis distance and the mean variance of the cluster (Woźniak et al. 2019), which allows for the assignment of meteorite to a specific group. The method described above gives satisfactory results, such that the validation of classification is about 88% (Figure 2).

  The measure introduced by us in the previous version of the 4M method, i.e., the level of similarity (S_clust), is only intuitive, so we continued looking for other more objective classification criteria based on the similarity of the studied mete­orite to individual subsets of the set of examined and classified meteorites constituting the database. Every idea of classification is to minimize the probability of the error of assigning observation to the wrong class (which is a function of the target). In the present case, observation stands for the vector (x) of the values of the subspectral areas of the studied meteorite, and the class is a set of measurements (database) of ordinary chondrites, which define subpopulations H, L and LL. We are looking for a discriminatory function that is to achieve the maximum for the assignment of the studied sample to a given subpopulation. A commonly used classification method is based on the Bayesian classification rule, which is formulated within the framework of statistical decision theory. It consists in assigning observation (x) to one of the subpopulations k (class, cluster p_k), for which the following condition is met:

        (1)

where P(p_k|x) – a posteriori probability that the observation x belongs to a subpopulation p_k. It is calculated from the Bayes formula:

        (2)

where k - number of subpopulations, p_k – a priori probability that the observation x belongs to a subpopulation p_k, and f(x|p_k) – the density function of the distribution of the (conditional) vector x in the subpopulation p_k. In the present case, individual sub­po­pulations (k=3) are described by 4-dimensional normal distributions with different means mk and covariance matrices Σ_k, so their density functions have the form:

        (3)

  By substituting f(x|p_k) into equation (2) and applying the logarithm (monotonic function) as well as omitting constant ele­ments, we obtain the following quadratic discriminant function (QDF):

        (4)

where p_k – a priori probability that the observation belongs to a subpopulation p_k.

Figure 3. BASE points classification – Bayes classification rule (pie charts) (validation, training ≡ testing set). The size of each circular graph is proportional to the maximum value of the discriminant function g_j(x). The portions in the pies are proportional to a posteriori proba­bi­lities for individual groups. The accuracy table collects the results of the classification of mete­orites from different groups ("true") related to recognized/predicted groups ("pred"). The correctness of classification with the revised 4M method is almost 95%.

  In the present case, the a priori probability of belonging to one of the three classes is 1/3 (this is also indicated by the statistics of falls and finds of ordinary chondrites (http://4mb.woreczko.pl/all.php). Using the definition of the Mahala­nobis distance (Mahalanobis 1936), we can conclude that the discriminant function g_k(x) depends on the Mahalanobis distance (d_M), the determinant of the covariance matrix (Σ_k), and the a priori probability (p_k):

        (5)

  We have tested this new classification criterion, i.e., the g_k(x) function, using our data­base. The validation of the results reaches almost 95% (Figure 3).

  Our previous classification criterion, using similarity function (S_clust), was based on an intuitive definition of the discriminant function. The new approach that we propose in the present paper, makes use of the Bayesian classification rule and has a strong theoretical basis, and hence provides better results.

Przykłady klasyfikacji metodą 4M

Dla sprawdzenia założeń zastosowaliśmy zaproponowaną przeze mnie metodę 4M do weryfikacji typów kilku znanych chondrytów zwyczajnych biorąc pod uwagę tylko powierzchnie spektralne podwidm mössbauerowskich. Wykorzystując opracowany przeze mnie → formularz można klasyfikować nieznane chondryty w oparciu tylko o dane mössbauerowskie! Taki był nasz cel!

Dla przetestowania metody (na podstawie naszego modelu → baza 4M-BASE) obliczyliśmy metodą 4M poziom podobieństwa (S_cluster) meteorytu Goronyo do poszczególnych typów. W klasycznej klasyfikacji mineralogicznej na wykresie ferrosilit versus fajalit punkt reprezentujący Goronyo znajduje się na granicy obszarów H i L. Obliczenia metodą 4M dla widma möss­ba­ue­row­skiego meteorytu Goronyo wykazały, że jest on podobny w 32% do typu H, 75% do typu L i 11% do typu LL (patrz tabela poniżej). Dodatkowe analizy mineralogiczne sugerują, że meteoryt Goronyo jest typu L, chociaż pierwotnie został on zgłoszony jako typ H w bazie Meteoritical Bulletin Database [Woźniak et al. 2019].^[1]

Poniżej w tabelach znajduje się kilka przykładowych wyników dla różnych znanych meteorytów: odległość Mahalanobisa (d_M) i poziom podobieństwa S_cluster [w %] do chondrytów zwyczajnych typu H, L i LL.

Przykładowe obliczenia przeprowadzone na podstawie bazy z listopada 2019 roku (4M-BASE-v1 – 59 meteorytów)

Przykłady klasyfikowanych meteoryty o znanych typach.

Same dobre trafienia!

Polecam samodzielne sprawdzenie → formularzem kilku nowych pomiarów meteorytów:

  Oued Sfayat, typ H5 (ol=33,3, pyr=16,5, met=36,4, tr=11,6);

  Gueltat Zemmour, typ L4 (ol=52,8, pyr=24,2, met=7,2, tr=15,2).

Metoda 4M będzie przez nas rozwijana (mam jeszcze kilka pomysłów do zaimplementowania), a baza widm mössbauerowskich chondrytów zwyczajnych będzie uzu­peł­nia­na o nowe dane doświadczalne. (Patrz → Najnowsza wersja bazy 4M-BASE-v2n oraz ilustracje)

Podziękowania

Autorzy pragną podziękować osobom, które przekazały do badań próbki meteorytów, są to: Marcin Cimała, Mike Gilmer, Ansgar Greshake, Łukasz Karwowski, Kazimierz Mazurek, Jarosław Morys, Krzysztof Socha, Robert Verish, Jan Woreczko.

Załącznik A

Istnieje wiele definicji różnych odległości (metryk) w matematyce. Oprócz najbardziej znanej odległości Euklidesa istnieją również inne metryki, np.: odległość Manhattanu, odległość Czebyszewa, odległość Hausdorffa oraz odległość Mahalanobisa (moja ulubiona ). Odległość Mahalanobisa stosowana jest zwykle w problemach statystycznych (np. w analizie skupień, Cluster Analysis; w analizie dyskryminacyjna, Discriminant Analysis). Stosujemy ją ilekroć chcemy znaleźć podobieństwo między nieznanym wektorem losowym a wektorem reprezentującym znany klaster.

DEFINICJA: Odległość Mahalanobisa d_M między badanym punktem X (n-wymiarowym wektorem zmien­nych), a klastrem opisanym wektorem wartości średnich X  oraz macierzą kowariancji Σ, jest zdefiniowana wzorem:

gdzie:  X  to wektor średnich wartości dla wszystkich zmiennych (tzw. centroid), a Σ  jest macierzą kowariancji klastra [Mahalanobis 1936].

Rys. A1. Przykład odległości Mahalanobisa (dM) dla przypadku 2-wymiarowego.

Rysunek A1 ilustruje ideę odległości Mahalanobisa (d_M) dla przypadku 2-wymiarowego. Na powyższym rysunku odległości Mahalanobisa od punktów 1 i 2 do „centrum klastra” są sobie równe, ale są one mniejsze niż odległość Mahalanobisa od punktu 3.

Natomiast na tym samym przykładzie mierząc odległość euklidesową (d) od punktów 1, 2 i 3 do „środka klastra”, otrzymamy inną relację:

Przykład różnicy między odległością euklidesową d a odległością Mahalanobisa d_M od dwóch różnych klastrów dla 2-wymiarowego przypadku pokazano na rysunku A2.

Rys. A2. Przykład różnicy między odległością euklidesową (d) a odległością Mahalanobisa (dM) w 2-wymiarowej przestrzeni dla dwóch klastrów. Na specjalnie dobranych na potrzeby ilustracji klastrów pokazano, jak ich kształt wpływa na wartości różnych miar odległości, co znajduje swoje odzwierciedlenie w odległość badanego punktu (X) od centroidów klastrów.

Załącznik B

Jak zdefiniowałem naszą „średnią wariancję” σ_aver. dla wielowymiarowego klastra (skupienia) opisanego macierzą kowariancji Σ?

  Założenie było takie, by definicja „średniej wariancji” była „odporna” na wpływ kształtu klastrów o bardziej egzo­tycznych formach (mocno wydłużonych, asymetrycznych, a nawet ameboidalnych), czyli takich, które mają niepożądaną większą tendencję do silniejszego „zagarniania czy też przyciągania” bliskich punktów, ale by nadal była ona („średnia wariancja”) proporcjonalna do wielkości (objętości) klastra. Zaproponowałem, że najlepszą miarą wielkości klastra będzie średnia geometryczna jego wariancji.

Nasz 4-wymiarowy klaster opisany jest macierzą kowariancji (Σ), ale z uwagi na występujące w niej korelacje pomiędzy parametrami, nie jest ona macierzą diagonalną (patrz → Tabele). Tak więc kształt (jej wariancje) „elipsoidy” 4D nie jest znany. Oznacza to, że wartości wariancji na przekątnej macierzy kowariancji Σ nie są wartościami, których szukamy. Szukamy wartości wariancji w takim układzie liniowych kombinacji zmiennych, w których wariancje te nie są skorelowane (patrz rysunek B1).

Rys. B1. Przykład klastra o niediagonalnej macierzy kowariancji (zmienne x są skorelowane) w pierwotnym układzie współrzędnych (X) i jego opis w przestrzeni składowych głównych (PC, Principal Components), gdzie przetransformowane zmienne (pc) nie są już skorelowane.

Aby wyznaczyć wartość „średniej wariancji” (σ_aver.) skorzystałem z własności macierzy kowariancji i analizy składowych głównych (PCA, Principal Components Analysis). Ponieważ macierz kowariancji jest macierzą symetryczną – więc można ją zdiagonalizować, gdyż zachodzi równanie: Λ = A^TΣA, gdzie A jest macierzą ortonormalną, natomiast Λ jest macierzą diagonalną [Morrison 1990; Krzanowski 2000]. Wartości na przekątnej macierzy Λ odpowiadają składowym głównym i są równe wartościom własnym (λ_i) (eigenvalues) macierzy kowariancji Σ. Możemy więc skorzystać z właściwości wyznacznika macierzy Λ:

gdzie λ_i to wartości własne zdiagonalizowanej macierzy Σ, które są proporcjonalne do wariancji wzdłuż składowych głównych [Krzanowski 2000] (patrz rysunek B1).

Do obliczenia stopnia podobieństwa S_cluster  (the level of similarity) chcemy zastosować średnią wariancję n-wymiarowego klastra. Zaproponowałem zdefiniować ją w taki sposób, by klastry o nietypowym kształcie miały „średnią wariancję” σ_aver. mniejszą od klastrów „regularnych” za jakie przyjęło się uważać, np. klasty w formie n-wymiarowej sfery.

  Wyobraźmy sobie dwa 3-wymiarowe klastry. Jeden z nich ma kształt podobny do dysku z wariancjami wzdłuż osi głównych równymi, na przykład λ₁ = 1,00, λ₂ = 4,00, λ₃ = 4,00, a drugi klaster ma kształt sferyczny o λ₁ = λ₂ = λ₃ = 3,00. Chcemy by klaster dyskowy miał „mniejszą” średnią wariancję. Jeśli zdefiniujemy „średnią wariancję” jako średnią arytmetyczną z λ_i, to dla tych dwóch przykładowych klastrów wartość będzie taka sama i wyniesie 3,00. Lepszą, i dla nas bardziej użyteczną średnią, wydaje się średnia geometryczna, która dla dowolnego zbioru liczb dodatnich a = (a₁,…, a_n) spełnia zależność:

średnia geometryczna a  ≤  średnia arytmetyczna a,

gdzie równość zachodzi tylko wtedy, gdy wszystkie liczby są równe (dla każdego i i j, a_i = a_j). W naszym przypadku odpowiada to klastrowi w kształcie sfery! Dla naszych dwóch przykładowych klastrów otrzymalibyśmy: dla klastra dyskowego – średnia geom. = 2,519, a dla klastra sferycznego – średnia geom. = 3,00. Dlatego do dalszych obliczeń wybrałem średnią geometryczną. Również jest tak, jak postulowałem na początku – jest ona proporcjonalna do objętości n-wymiarowego klastra!!

  Stąd przyjęta (postulowana) przeze mnie „średnia wariancja” σ_aver. (dla przestrzeni n-wymiarowej) zdefiniowana w metodzie 4M jest równa średniej geometrycznej wartości własnych macierzy kowariancji Σ:

Czyli jest to 2n-ty pierwiastek wyznacznika macierzy kowariancji det(Σ), gdzie n jest wymiarem przestrzeni parametrów (tutaj n = 4).

Załącznik M

Własności podwidm dla minerałów (zawierających jony Fe) występujących w meteorytach (patrz → Minerały w meteorytach):

4M-BASE – tabele (listopad 2019 roku: 4M-BASE-v1 – 59 meteorytów)

Zbiór parametrów definiujących naszą bazę 4M-BASE – liczebność prób (n), średnie i macierze kowariancji. Pierwsza wersja bazy została skonstruowana w oparciu o 59 widma meteorytów znanych typów (4M-BASE-v1, listopad 2019 r.)  i opubli­ko­wana w 2019 roku w czasopiśmie Meteoritical and Planetary Science [Woźniak et al. 2019].

  Tabela pierwsza. Wartości średnie (E) czterech parametrów (ol, pyr, met i tr) oraz ich odchylenia standardowe (Dev) [%].

  Tabela druga. Nieobciążony estymator macierzy kowariancji (Cov, S).

  Tabela trzecia. Macierz korelacji (Corr) (pogrubioną czcionką wyróżnione są wartości korelacji dla pary oliwin vs. faza metaliczna – patrz rysunek). Oraz wartość wyznacznika (det) (determinant) estymatora macierzy kowariancji i jej wartości własne (eigenvalues).

Klaster H – chondryty zwyczajne typu H

Na definicję klastra H składają się wyniki pomiarów meteorytów:^[4]
Allegan (H5), Bassikounou (H5), Buzzard Coulee (H4), Carancas (H4-5), Didwana (H5), Gujargaon (H5), Grzempach (H5), Juancheng (H5), Kidairat (H6), Kosice (H5), Noblesville (H4-6), Ochansk (H4), Pułtusk (H5), Richardton (H5), Tamdakht (H5), Torino (H6), Vengerovo (H5), Wuan (H6), ×2^[5] Xingyang (H6), Zag (H3-6), Zvonkov (H6).

det(Cov^H) = 7643,096498;

Wartości własne (eigenvalues) λ_i: 73,124869; 13,192740; 7,591481; 1,043621.

Klaster L – chondryty zwyczajne typu L

Klaster LL – chondryty zwyczajne typu LL

4M-BASE-v2n – najnowsza wersja (ilustracje)  .

Abstract

The 4M method aims to determine the type of equilibrated ordinary chondrite only on the basis of the Mössbauer spectrum of the inves­ti­gated meteorite. Mössbauer spectrum of non-weathered ordinary chondrite is comprised of four sub-spectra: two doublets and two sextets. One of the doublets consists of a signal from iron present in olivine and the other consists of a signal from iron present in pyroxe­ne. Sextets on the other hand, contain signals from magnetically ordered iron. One sextet is related to the metallic phase (kamacite, taenite), whereas the second is related to troilite. A third of doublets, which emerges in weathered ordinary chondrites, is related to products of the oxidation of iron present in metallic phase. The spectral areas of olivine, pyroxenes, metallic phase and troilite, which were obtained from Mössbauer spectrum are proportional to the number of iron atoms present in relevant mineral phases. Some Möss­bauer groups were inspired by this fact to construct different methods to determine the type (H, L, or LL) of investigated meteorites (Gałązka-Friedman et al. 2019, Hyp. Inter. 241(1)). However, these methods, based on subjective criteria, were only qualitative. Our group elaborated a quantitative method, which is based on objective criteria. We called it the "4M method" (where M are derived from meteorites, Mössbauer spectroscopy, multidimensional discriminant analysis (MDA), Mahalanobis distance) (Woźniak et al. 2019, MaPS).
  This method was using only the Mössbauer experimental data, to which it applied advanced statistical methods. The base, which was created from Mössbauer data, consisted of three clusters H, L, LL. These clusters were constructed with sets of 4-dimensional vectors. The vectors are comprised of spectral areas of Mössbauer spectrum: ol (value propor­tio­nal to iron present in olivine), pyr (value pro­portional to iron present in pyroxene), met (value propor­tio­nal to iron present in metallic phase), tr (value propor­tio­nal to iron present in troilite). To determine the type of investigated ordinary chondrite, its ol, pyr, met and tr values with average values of variables obtained for clusters H, L and LL need to be compared. The comparison can be performed with the use of MDA and Mahalanobis distance. Once Mahalanobis distance of the investigated meteoriteis is known, the level of similarity to three types of ordinary chondrites can be calculated.
  Examples of such calculations were performed for seven ordinary chondrites: Goronyo, Carancas, New Concord, NWA 7733, Leoncin, Sołtmany and Pułtusk. They were made with the use of the new base composed of 62 non-weathered ordinary chondrites. All results obtained with the 4M method yielded results consistent with traditional mineralogical methods.

Zobacz również

• Krzemiany (Silicates). Przykładowe wyniki analizy składu fazy krzemianowej w chondrycie zwyczajnym Goronyo.

• Żelazo (podział chondrytów)

• Minerały w meteorytach (Meteorite minerals)

• Mikrosonda (Microprobe)

• Najnowsza wersja bazy 4M-BASE-v2n  (ilustracje)
  (wersja 1.0 z MaPS:  BASE-v1 | ilustracje | formularz)

Przypisy

[1]  (Woźniak et al. 2019, MaPS) Abstract: Mössbauer spectra of equilibrated ordinary chondrites consist of two doublets due to para­magnetic iron present in olivines and pyroxenes and two sextets due to magnetically ordered iron present in metallic phases and troilite. The spectral areas of the diffe­rent mineralogical phases found by Mössbauer spectroscopy in meteorites are proportional to the number of iron atoms in this mineral phase. This property of Mössbauer spectra can be the basis for constructing a method for the classification of ordinary chondrites. This idea was first explored at the Mössbauer Laboratory in Kanpur. This group suggested a qualitative method based on 2-dimensional plots of Mössbauer spectral areas and thus classified properly some meteorites. We construc­ted a quantitative method using Mössbauer spectral areas, multidimensional discriminant analysis, and Mahalanobis distance (4M method) to determine the probability of a meteorite to be of type H, L, or LL. Based on 59 Mössbauer spectra, we calculated by the 4M method, S_cluster, the level of similarity of the Goronyo meteorite to the clusters. On the plot of ferrosilite versus fayalite, the point representing Goronyo is located on the border between H and L areas. Calculated by the 4M method, the meteorite Goronyo is 32% similar to type H, 75% to type L, and 11% to type LL. Additional mineralogical analyses suggested that the Goronyo meteorite would be classified as type L, although it was originally reported as type H in the Meteoritical Bulletin Database.

[2]  W zwietrzałych meteorytach występuje jeszcze jon żelaza Fe⁺³ w postacie tlenków i wodorotlenków żelaza.

[3]  Nowy polski meteoryt Leoncin (typ LL4-6). W jego opisie w Meteoritical Bulletin Database wspomniano o klasyfikacji metodą 4M („...Mössbauer spectroscopy confirmed LL classification”)! Więcej na wiki.meteoritica.pl – Leoncin.

[4]  Podkreślono nazwy meteorytów zmierzonych w laboratorium na Politechnice Warszawskiej, pozostałe pomiary pochodzą z literatury [Woźniak et al. 2019].

[5]  Z niektórych meteorytów wykonano więcej niż jedną próbkę (holderków) do pomiarów.

[6]  W chondrytach zwyczajnych występuje więcej faz mineralnych zawierających jony żelaza (Fe⁰, Fe²⁺). Są jeszcze, np.: chromit, augit, tetrataenit, antytaenit, awaruit; patrz → Minerały w meteorytach (Meteorite minerals).

[7]  Już wcześniej miałem kontakt z prof. Jolantą Gałazką-Friedman i dr. Karolem Szlachtą, ale mój udział sprowadzał się do przekazywania próbek do badań. Wówczas „temat” mnie nie porwał

[8]  Ważnymi, ale często pomijanymi w spektroskopii mössbauerowskiej, są fazy tlenków (spineli). Ich udział w widmie wynosi kilka procent, a czasami nawet kilkanaście procent. Najpopularniejszy jest chromit (singlet). Również wiele prac wskazuje na znaczną zawartość innego spinelu hercynitu (dublet) (Maksimova et al. 2019).

[9]  W oliwinie i piroksenie ze względu na położenie jonów metali (Fe i Mg) w sieci kryształu w dwóch różnych położeniach, M1 i M2, ich dublety składają się w rzeczywistości z par dubletów. Więcej informacji w publikacji Dyar et al. 2009.

Źródła (sources)

Bogusz Patrycja, Gałązka-Friedman Jolanta, Brzózka Katarzyna, Jakubowska Martyna, Woźniak Marek, Karwowski Łukasz, Duda Przemysław, (2019), Mössbauer spectroscopy as a useful method for distinguishing between real and false meteorites, Hyperfine Interactions, 240(1), 2019, ss. 11. Plik doi.

Dyar M.D., et al., (2009), Spectroscopic characteristics of synthetic olivine: An integrated multi-wavelength and multi-technique approach, American Mineralogist, 94, 2009, s. 883-898. Plik doi.

Gałązka-Friedman Jolanta, Woźniak Marek, Duda Przemysław, Jakubowska Martyna, Bogusz Patrycja, Karwowski Łukasz, (2019), Próby klasyfikowania chondrytów zwyczajnych przez zastosowanie spektroskopii mössbauerowskiej (Attempts of classification of ordinary chondrites by application of Mössbauer spectroscopy), Acta Soc. Metheor. Polon., 10, 2019, s. 23-28. Plik ASMP.

Gałązka-Friedman Jolanta, Woźniak Marek, Bogusz Patrycja, Jakubowska Martyna, Karwowski Łukasz, Duda Przemysław, (2019), Application of Mössbauer spectroscopy for classification of ordinary chondrites – different database and different methods, Hyperfine Interactions, 241(1), 2019, ss. 12. Plik doi.

Koblitz Jörn, MetBase. Meteorite Data Retrieval Software, Version 7.3 (CD-ROM), Ritterhude, Germany 1994-2012.

Woźniak Marek, Gałązka-Friedman Jolanta, Duda Przemysław, Jakubowska Martyna, Rzepecka Patrycja, Karwowski Łukasz, (2019), Application of Mössbauer spectroscopy, multidimensional discriminant analysis, and Mahalanobis distance for classification of equilibrated ordinary chondrites, Meteoritics & Planetary Science, vol. 54(8), 2019, s. 1828-1839.^[1] Plik doi.

Maksimova Alevtina A., Chukin Andrey V., Felner Israel, Oshtrakh Michael I., (2019), Spinels in Meteorites: Observation Using Mössbauer Spectroscopy, Minerals, 9(1), 2019. Plik doi.

Grandjean Fernande, Long Gary J., (2021), Best Practices and Protocols in Mössbauer Spectroscopy, Chem. Mater., 33(11), 2021, s. 3878-3904. Plik doi.

Literatura: [Fredriksson i Keil 1964], [Krzanowski 2000], [Mahalanobis 1936], [Mason 1962], [Morrison 1990] – patrz → [Woźniak et al. 2019]

Dane literaturowe:
[1] Verma et al. 2003, MaPS, doi; [2] Lipka et al. 2013, HI, doi; [3] Oshtrakh et al. 2008, MaPS, doi; [4] Ortalli et al. 1990, HI, doi; [5] Verma et al. 2002, HI, doi; [6] Zhang et al. 1994, HI, doi; [7] Abdu et al. 1997, MaPS, doi  (patrz → [Woźniak et al. 2019])
[8] Maksimova A.A., Oshtrakh M.I., Petrova E.V, Grokhovskya V.I., Semionkina V.A., (2017), Comparison of iron-bearing minerals in ordinary chondrites from H, L and LL groups using Mössbauer spectroscopy with a high velocity resolution, Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 172, 2017, s. 65–76. Plik doi.
[9] Maksimova A.A., Oshtrakh M.I., Felner I., Chukin A.V., Karabanalov M.S., Semionkin V.A., (2017), Möossbauer spectroscopy of NWA 6286 and NWA 7857 ordinary chondrites, Journal of Molecular Structure, 1140, s. 122-126. Plik doi.
[10] Maksimova A.A., et al., (2020), Characterization of the matrix and fusion crust of the recent meteorite fall Ozerki L6, Meteoritics & Planetary Science, vol. 55(1), 2020, s. 231-244. Plik doi.
[11] Maksimova A.A., et al., (2020), Characterization of Kemer L4 meteorite using Raman spectroscopy, X-ray diffraction, magnetization measurements and Mössbauer spectroscopy, Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 242, 2020. Plik doi.
[12/x] Maksimova A.A., et al., (2021), Applications of Mössbauer Spectroscopy in Meteoritical and Planetary Science, Part I: Undifferentiated Meteorites, Minerals, 11(6), 2021. Plik doi. I inne (x) cytowane tam publikacje.

New D. upper-right